Реферат: Законы сохранения как отражение симметрии в физике

Рассмотрим симметрию пространства. Есть существенная разница между координатной системой на плоскости и в пространстве. Координатные системы на плоскости всегда могут быть полностью совмещены друг с другом. Действительно, пусть совмещены абсциссы. Тогда возможны два случая: либо ординаты тоже совмещены, либо они направлены в противоположные стороны. В первом случае нечего больше доказывать, а во втором случае надо повернуть одну из систем вокруг абсциссы на 180, выведя ординату из плоскости.

Теперь рассмотрим, как обстоит дело в пространстве. Две оси легко совместить только что описанным способом. После этого третьи оси могут иметь либо одинаковое, либо противоположное направление. В последнем случае их невозможно совместить никаким поворотом. Ведь если повернуть систему вокруг оси абсцисс, то ординаты тоже повернутся вместе с третьей осью. Следовательно, если две из трех осей совпадают, а третьи направлены противоположно, то такие координатные системы невозможно совместить. По аналогии с руками координатные системы называются правой и левой. Отличать их следует так. Обычный «правый» винт направляют (мысленно) по оси Z. Тогда, если вращать головку винта от оси Х к оси Y по часовой стрелке, то сам винт будет перемещаться по оси Z. Правый винт, отраженный в зеркале, становится левым. Законы механики совершенно тождественно формулируются в обеих системах координат.

Всегда следует помнить, что симметрия того или другого рода есть свойство определенных законов движения, а не абстрактного пространства, как его представляют себе по учебникам геометрии. Всякие физические законы выражают известное приближение к истине: абсолютных законов пока нет, и мы не знаем, существуют ли они. Поэтому свойства симметрии являются приближенными в той же мере, как сами законы движения, обладающие этими свойствами.

Столь осторожное высказывание относится к законам, которые еще не уточнены: мы не можем предугадать, в какую сторону пойдет уточнение. Но бывают случаи, когда свойства симметрии не нарушаются при переходе к более детальным закономерностям движения. Так, все что сказано о симметрии пространства и времени в ньютоновской механике, целиком переносится в квантовую механику. Особенно важно при этом свойство симметрии относительно правого левого: в квантовой механике из него получается новый закон сохранения, который нельзя формулировать в классической механике.

Пространство обладает еще одним видом симметрии – относительно поворотов координатных систем. Достаточно далеко от всех тяготеющих тел все точки пространства равноценны, равно как все прямые, проведенные через любую точку. Вокруг любой прямой можно повернуть координатную систему на любой угол, и повернутая система будет во всех отношениях равноценна первоначальной. Симметрию относительно поворотов называют изотропией, относительно переносов – однородностью.

Может показаться, то рассуждение о свойствах симметрии пространства, основанное на законах движения, ничего не прибавляет к нашим действительным знаниям о движении. Все свойства пространства заключены в геометрии Евклида, которой механика пользуется от своего зарождения и по сей день. Но интуитивное чувство реальности, с которым связано применение геометрии Евклида, основано в конечном счете на повседневном опыте. Насколько он хорош в масштабе Солнечной системы? А во всей вселенной? Ньютон высказался осторожно в этом смысле, чувствуя, что свойства пространства могут быть определены только физически, а не чисто геометрически. Но последующие поколения ученых были более догматичны.

По-новому подошел к вопросу только Эйнштейн, который показал, что пространство удовлетворяет аксиомам евклидовой геометрии приближенно. Как раз отклонение от евклидовости воспринимаются как действие сил тяготения. Но механика Эйнштейна существенно уточняет ньютоновскую. В рамках механики Ньютона пространство однородно и изотропно.

Что же все-таки мы получаем, привлекая свойства симметрии пространства в явном виде при анализе законов механики? Реальное удобство от пользования понятиями симметрии заключено в том, что из них легко и непринужденно вытекают все механические законы сохранения. Покажем, что с каждым свойством симметрии связан закон сохранения.

????? II. ?????? ?????????? ??? ????????? ????????? ? ?????? 1. ??????? ͸???

Немецкий математик Эмми Нётер в 1918 году математически доказала связь между законами сохранения и симметрией, которой обладают в физике законы природы. По выражению Феймана, «среди наиболее мудрейших и удивительнейших вещей в физике эта связь - одна из самых интересных и красивых».

Теорема Нётер утверждает, что для физической системы, уравнение движения которой имеет форму системы дифференциальных уравнений и могут быть получены из вариационного принципа, каждому однопараметрическому непрерывному преобразованию , преобразуется один параметр - t, или q, или , оставляющему вариационный функционал инвариантным, соответствует один дифференциальный закон сохранения.

Теорема Нетер заключается в том, что существует физическая величина, которая называется действие

где - функция Лагранжа, с помощью которой описывается некоторая система. Действие S имеет экстремум вблизи истинной траектории, вариация действия S вдоль истинной траектории остается неизменной, т.е. S=0. Вариация действия зависит от вариации начала отсчета времени t и вариации начала координат q таким образом

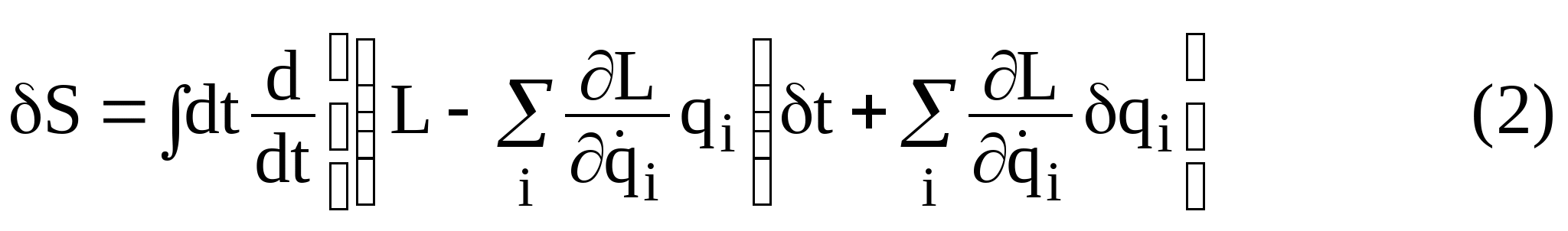
Можно показать из того, что S=0 следует

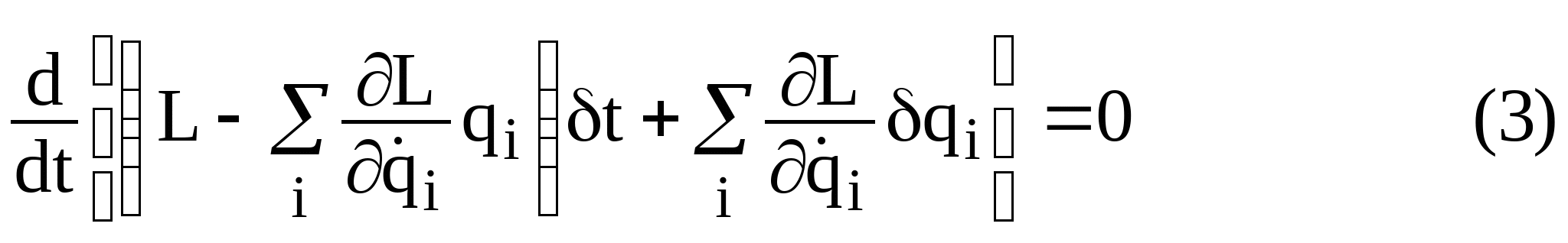
Величина

сохраняется во времени. Это и есть точное утверждение теоремы Нетер.

В упрощенной формулировке теорема Нётер гласит, что если свойства системы не меняются от какого-либо преобразования переменных, то этому соответствует некоторый закон сохранения. Теорема Нётер - самое простое и универсальное средство, позволяющее находить законы сохранения в классической механике, квантовой механике, теории поля и т.д. Так, например, инвариантность действия для системы по отношению к сдвигам времени (что отвечает физическому представлению об однородности времени) влечёт за собой, по теореме Нётер, закон сохранения энергии. Из однородности пространства (инвариантности действия по отношению к пространственным сдвигам) вытекает закон сохранения импульса. Подобным же образом из изотропности пространства (т.е. равноценности всех пространственных направлений и связанной с этим инвариантности действия относительно вращения системы координат в пространстве) следует закон сохранения момента.

Таким образом, из физического представления об однородности и изотропности пространства-времени следует, что для всякой замкнутой системы должны существовать семь фундаментальных сохраняющихся величин: энергия, компоненты импульса (три величины) и моментов (три величины).

При наличии в системе симметрий другого рода (не связанных с пространством-временем) теорема Нётер позволяет построить и другие сохраняющиеся величины (например, электрический заряд и т.п.). Особо важное значение теорема Нётер принимает в квантовой теории поля, где часто вытекающие из наличия группы симметрий законы сохранения являются единственным источником информации о свойствах системы.

2. ???????????? ?????? ?????????? 2.1. ????? ?????????? ???????

Начнём применение теоремы Нётер к универсальным преобразованиям симметрии с рассмотрения сдвига во времени. Чтобы получить это преобразование надо, очевидно, считать за независимый и постоянный параметр преобразования, .

Уравнение (3) иметь вид

Оно означает, что как следствие инвариантности действия относительно временного сдвига сохраняется динамическая величина

Эта величина называется энергией системы.

Если функцию Лагранжа можно представить в виде разности (Т‑U) кинетической и потенциальной энергий