Реферат: Затухание ЭМВ при распространении в средах с конечной проводимостью
Таким образом, при ![]() волновое число k комплексно. Обозначим k=a+ib, где a — фазовая константа, b — коэффициент затухания. Тогда
волновое число k комплексно. Обозначим k=a+ib, где a — фазовая константа, b — коэффициент затухания. Тогда
![]()
![]()
![]() (2.3)
(2.3)
Следовательно, при р=iw имеет место волновой процесс с затуханием, если ![]() .
.
Исследуем фазовую скорость волны в среде с конечными e и s. Поскольку волновое число комплексно: k=a+ib, имеем
![]()
(![]() 2 считаем равным нулю).
2 считаем равным нулю).
В общем случае ![]() 1 также комплексно:
1 также комплексно: ![]() ,
,
![]()
где a, b, ![]() , q — действительные числа. Отсюда получаем выражение фазовой скорости
, q — действительные числа. Отсюда получаем выражение фазовой скорости
![]()
Действительно, так как ![]() представляет скорость, с которой движется плоскость постоянной фазы
представляет скорость, с которой движется плоскость постоянной фазы
![]() =const
=const
то
![]()
откуда
![]()
Для определения степени затухания и фазовой скорости нужно вычислить a и b. Из уравнений (2.3) получаем
![]()
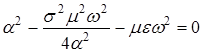
Введем обозначение
![]()
тогда
![]()
или

Здесь нужно оставить знак +, так как a — действительное число
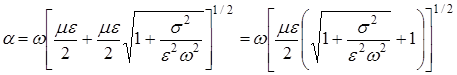 (2.4)
(2.4)
Аналогично получим для b
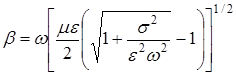 (2.5)
(2.5)
Отсюда находим фазовую скорость
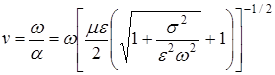 (2.6)
(2.6)
Зависимость фазовой скорости от частоты сложная: если e, m, s не зависят от частоты, то с увеличением w фазовая скорость увеличивается, т. е. в сложной волне гармоники убегают вперед.
Рассмотрим зависимость поглощения b, определяемого равенством (2.5), от электрических характеристик среды. Член ![]() представляет отношение
представляет отношение ![]() , так как
, так как ![]() . Следовательно,
. Следовательно,
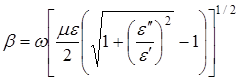
Но ![]() , поэтому при tgd<<1
, поэтому при tgd<<1
![]()
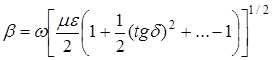
Ограничившись двумя членами разложения, получим
![]() (2.7)
(2.7)
Следовательно, по поглощению волны можно определить tgd:
![]()
![]()
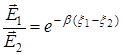
при ![]() (единица длины) получаем
(единица длины) получаем
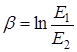
Измеряется b в неперах

или в децибелах

где P — мощность.