Шпаргалка: Множественная регрессия и корреляция

Среднедневной душевой доход,

руб., y

86,8 11,44 - Среднедневная заработная плата одного работающего, руб., x1 54,9 5,86

Средний возраст безработного,

лет, x2

33,5 0,58

Требуется:

1. Построить уравнение множественной регрессии в стандартизованной и естественной форме; рассчитать частные коэффициенты эластичности, сравнить их с b1 и b2 , пояснить различия между ними.

2. Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции, сравнить их с линейными коэффициентами парной корреляции, пояснить различия между ними.

3. Рассчитать общий и частные F-критерии Фишера.

Решение

1. Линейное уравнение множественной регрессии y от х1 и х2 имеет вид: . Для расчета его параметров применим метод стандартизации переменных и построим искомое уравнение в стандартизованном масштабе: .

Расчет b-коэффициентов выполним по формулам

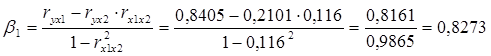
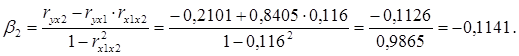
Получим уравнение:

Для построения уравнения в естественной форме рассчитаем и , используя формулы для перехода от к :

Значение определим из соотношения

Для характеристики относительной силы влияния и на рассчитаем средние коэффициенты эластичности:

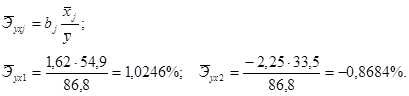
С увеличением средней заработной платы на 1% от ее среднего уровня средний душевой доход возрастает на 1,02% от своего среднего уровня; при повышении среднего возраста безработного на 1% среднедушевой доход снижается на 0,87% от своего среднего уровня. Очевидно, что сила влияния средней заработной платы на средний душевой доход оказалась больше, чем сила влияния среднего возраста безработного . К аналогичным выводам о силе связи приходим при сравнении модулей значений и :

.

Различия в силе влияния фактора на результат, полученные при сравнении и , объясняются тем, что коэффициент эластичности исходит из соотношения средних: а -коэффициент - из соотношения средних квадратических отклонений:.

2. Линейные коэффициенты частной корреляции здесь рассчитываются по рекуррентной формуле: