Шпаргалка: Высшая математика, интегралы шпаргалка

Пусть требуется вычислить интеграл , где . Введём новую переменную формулой: , где функция дифференцируема на и имеет обратную , т.е. отображение на - взаимно-однозначное. Получим: . Тогда . Т.е. вычисление интеграла сводится к вычислению интеграла (который может оказаться проще) и последующей подстановке .

Пример: Вычислить .

, откуда: .

Интегрирование по частям . Пусть - дифференцируемые функции, тогда справедлива формула: , или короче: . Эта формула используется в тех случаях, когда подынтегральное выражение можно так представить в виде , что интеграл вычисляется проще исходного.

Пример: Вычислить .

Положим . Тогда . В качестве выберем первообразную при . Получим . Снова . Тогда . Окончательно получим: .
Замечание 26.5: Иногда при вычислении интеграла методом интегрирования по частям получается зависимость: . Откуда можно получить выражение для первообразной: .

Интегрирование рациональных функций

Постановка задачи:

1).	2).
3).

т.е. все задачи сводятся к задаче B.2).

Теорема 1: Пусть , тогда, если: , где , то Из этой теоремы следует, что для интегрирования любой рациональной функции необходимо уметь интегрировать следующие функции:

1.	2.	3.	4.	5.
6.	7.	8.	9.	10. .

Интегрирования дробно-линейных и квадратичных иррациональностей

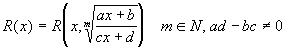
Сделав подстановку: , получим: .

тогда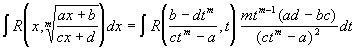

a). Подстановки Эйлера.

1). Корни многочлена - комплексные, сделав подстановку: , получим: .

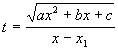2). Корни многочлена - действительные: . Подстановка: , получаем: .

b). Подстановка: , далее, если:

1). подстановка -	2). подстановка -
3). подстановка -

c).

Если подстановка -

Интегрирование функций, рационально зависящих от тригонометрических

Универсальная подстановка: , тогда:

подстановка:

или - нечётные: вносим функцию при нечётной степени под знак дифференциала

Интегрируется по частям

Неопределенный интеграл

Определение 26.1: Функция называется первообразной для функции на , если: .