Шпаргалка: Высшая математика, интегралы шпаргалка
Равномерная непрерывность
Определение 28.7: Функция ![]() называется равномерно непрерывной на множестве
называется равномерно непрерывной на множестве ![]() , если:
, если: ![]() . (в отличие от критерия Коши:
. (в отличие от критерия Коши: ![]() ).
).
Пояснение: ![]() Пусть:
Пусть: ![]() . Тогда:
. Тогда: ![]() Т.е. функция
Т.е. функция ![]() не является равномерно непрерывной на множестве
не является равномерно непрерывной на множестве ![]() .
.
Теорема 28.3: Непрерывная на отрезке функция – равномерно непрерывна на нём.
Классы интегрируемых функций
Теорема 28.4: Непрерывная на отрезке функция – интегрируема на нём.
Теорема 28.5: Монотонная на отрезке функция – интегрируема на нём.
Теорема 28.5: Если функция ![]() определена и ограничена на отрезке
определена и ограничена на отрезке ![]() , и если
, и если ![]() можно указать конечное число интервалов, покрывающих все точки разрыва этой функции на
можно указать конечное число интервалов, покрывающих все точки разрыва этой функции на ![]() . Причём общая длина этих интервалов меньше
. Причём общая длина этих интервалов меньше ![]() . То
. То ![]() - интегрируема на
- интегрируема на ![]() .
.
Замечание: Очевидно, что если ![]() - интегрируема на
- интегрируема на ![]() , а
, а ![]() отличается от
отличается от ![]() только в конечном числе точек, то
только в конечном числе точек, то ![]() - интегрируема на
- интегрируема на ![]() и
и 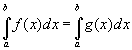 .
.
Существование первообразной
Определение 28.9: Пусть ![]() - интегрируема на
- интегрируема на ![]() ,
, ![]() , тогда:
, тогда: ![]() функция
функция ![]() интегрируема на
интегрируема на ![]() и функция
и функция 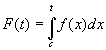 называется интегралом с переменным верхним пределом, аналогично функция
называется интегралом с переменным верхним пределом, аналогично функция 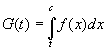 - интеграл с переменным нижним пределом.
- интеграл с переменным нижним пределом.
Теорема 28.6: Если функция ![]() - непрерывна на
- непрерывна на ![]() , то у неё существует на
, то у неё существует на ![]() первообразная, одна из которых равна:
первообразная, одна из которых равна: 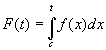 , где
, где ![]() .
.
Замечание 1: Из дифференцируемости функции ![]() следует её непрерывность, т.е.
следует её непрерывность, т.е. ![]()
Замечание 2: Поскольку 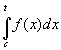 - одна из первообразных
- одна из первообразных ![]() , то по определению неопределённого интеграла и теореме о разности первообразных:
, то по определению неопределённого интеграла и теореме о разности первообразных: 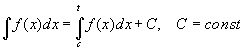 . Это связь между определённым и неопределённым интегралами
. Это связь между определённым и неопределённым интегралами
Интегрирование подстановкой
Пусть для вычисления интеграла 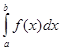 от непрерывной функции сделана подстановка
от непрерывной функции сделана подстановка ![]() .
.
Теорема. Если 1. Функция ![]() и ее производная
и ее производная ![]() непрерывны при
непрерывны при ![]()
2. множеством значений функции ![]() при
при ![]() является отрезок [a;b]
является отрезок [a;b]
3. ![]() , то
, то 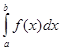 =
=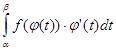 .
.
Док-во: Пусть F(x) есть первообразная для f(x) на отрезке [a;b]. Тогда по формуле Ньютона-Лейбница 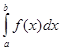 =
=![]() . Т.к.
. Т.к. ![]() , то
, то ![]() является первообразной для функции
является первообразной для функции ![]() ,
, ![]() . Поэтому по формуле Ньютона-Лейбница имеем
. Поэтому по формуле Ньютона-Лейбница имеем
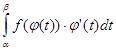 =
=![]()
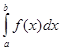 .
.
Формула замены переменной в определенном интеграле.
1. при вычислении опред. интег-ла методом подстановки возвращаться к старой переменной не требуется;
2. часто вместо подстановки ![]() применяют подстановку t=g(x)
применяют подстановку t=g(x)
3. не следует забывать менять пределы интегрирования при замене переменных.
Интегрирование заменой переменной .
а). Метод подведения под знак дифференциала
Пусть требуется вычислить интеграл ![]() . Предположим, что существуют дифференцируемая функция
. Предположим, что существуют дифференцируемая функция ![]() и функция
и функция ![]() такие, что подынтегральное выражение
такие, что подынтегральное выражение ![]() может быть записано в виде:
может быть записано в виде:
![]() .
.
Тогда: ![]() . Т.е. вычисление интеграла
. Т.е. вычисление интеграла ![]() сводится к вычислению интеграла
сводится к вычислению интеграла ![]() (который может оказаться проще) и последующей подстановке
(который может оказаться проще) и последующей подстановке ![]() .
.
Пример: Вычислить ![]() .
.
![]() .
.
Подстановка: ![]() .
.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--