M – Точка встречи

Эта окружность называется окружностью Апполония, а точка А (самая удалённая точка на прямой PE) называется точкой Апполония.

Доказательство: Обозначим через vp – скорость преследователя, а через ve скорость убегающего игрока, тогда ve*|EM|=vp*|PM|. Выберем на плоскости систему координат x0y таким образом, чтобы E(0)=(0,0), P=(0, – b), тогда

|EM|= Ö x² +y² |PM|= Ö x² +(y+b)²

Подставив это выражение в первое соотношение получаем

ve*Ö x² +y² =vp*Ö x² +(y+b)² .

Возведём обе части в квадрат и получим

ve² * [x² +y² ]=vp² *[x² +(y+b)² ]

(ve² – vp² )*x² + (ve² – vp² )*y² – 2*b*vp² *y = b² *vp²

Разделим это выражение на (ve² – vp² ) сгруппируем. Получим следующее:

x² + (y – b*vp² /(ve² – vp² ))² = (ve*vp*b)² /(ve² – vp² )²

Это и есть уравнение окружности, что и требовалось доказать.

Окружность Апполония и точка Апполония представляют собой очень важные объекты, имеющие самое серьёзное применение в теории преследования на плоскости. С их помощью можно оценивать различные величины, характеризующие процесс преследования и получать траектории движения игроков. Приведём в подтверждение несколько маленьких теорем.

Теорема 1: Пусть убегающий игрок и преследователь перемещаются по своим полупрямым. Их положение зависит от времени. Обозначим его через P(t), E(t) тогда любой отрезок [P(t), E(t)] параллелен отрезку [P(0), E(0)]. На рисунке внизу эти отрезки выделены:

Теорема 2: Пусть убегающий игрок движется по прямой пересекающей окружность Апполония в точке М, движение начинается из точки Е со скоростью V. Тогда преследователь не может встретится с убегающим раньше чем за время равное |EM| / V

Значение этой теоремы трудно переоценить, так как она утверждает, что окружность Апполония – это геометрическое место точек в которых происходит гарантированная встреча при оптимальном поведении обоих игроков. Не раньше и не позже. А так как оптимальное время преследования одна из главных целей анализа теории, то становится ясным, почему нужно уметь строить окружность Апполония

3 Стратегия параллельного сближения

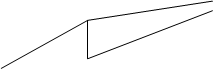
А теперь рассмотрим пример стратегии погони. Цель стратегии параллельного сближения заключается в том, чтобы обеспечить преследователю максимальное сближение с убегающим игроком. Ниже на картинке показаны возможные траектории преследователя и убегающего игрока при использовании стратегии параллельного преследования.

Обратите внимание, что отрезки соединяющие точки, в которых произошла смена направления движения, параллельны друг другу. Этот факт и дал название стратегии.

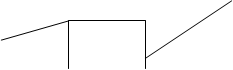Почему именно так. Рассмотрим какой-либо участок движения на котором оба участника погони движутся по прямым. Их поведение оптимально, это означает, что они движутся к точке встречи расположенной на соответствующей окружности Апполония (обозначим её А1) и это означает (см. выше), что любые два отрезка соединяющие положение убегающего и догоняющего параллельны.

Пусть теперь убегающий игрок сменил направление. Иначе говоря он перешел к другой окружности Апполония (обозначим её А2). Пусть А точка в которой сменил направление убегающий игрок и В точка в которой сменил направление догоняющий игрок. Тогда отрезок АВ конец пути по траектории на А1 и начало пути по траектории А2. Следовательно любой отрезок на траектории А1 параллелен АВ и в то же время любой отрезок на траектории А2 также параллелен АВ. Таким образом, параллельность отрезков соединяющих соответствующие точки на траектории убегающего и догоняющего игроков сохраняются и при смене направления движения.

Один кролик и несколько лис

Вспомним задачу с которой началась работа. Один кролик пытается убежать от группы лисиц. Известно, что кролик бегает быстрее лисиц. Ситуация в которой все лисицы находятся в одной полуплоскости от кролика можно считать неинтересной. Его скорость выше и он непременно убежит. Какой-то шанс у лисиц появляется, если им каким-либо образом удастся кролика окружить. Вот так:

Конечно, сам по себе факт окружения кролика успеха лисам не гарантирует. Совершенно очевидно, что нужно ещё что-то. Нужно видимо какое-то специальное отношение расстояний, отношение скоростей. В общем, между различными факторами образующими ситуацию, необходима какая-то закономерность.

Основой, известного нам, математического аппарата является окружность Апполония, но как мы помним из предыдущей лекции она строилась из тех соображения, что преследователь быстрее убегающего, в противном случае множество точек встречи просто пустое. Поэтому на первый взгляд использовать окружность Апполония не получится.

Проведём небольшое формальное преобразование. Пусть кролик будет преследователем, а лиса убегающим, а чтобы эту новую задачу свести к предыдущей добавим в условие, что все направления движения от кролика для лисы запрещены и двигаться она может только к кролику, а кролику разрешено движение только по прямой из исходной точки. С точки зрения здравого смысла такая постановка абсурдна, но как математики, мы имеем право так поступить. Новая задача будет выглядеть так: Несколько лис окружили кролика который пытается поймать хотя бы одну. Лисы не возражают и ведут себя так, чтобы максимально облегчить задачу кролика. Вопрос, при каких условиях на любом направлении движения кролика по прямой, лисы смогут осуществить встречу кролика хотя бы с одной лисой.

В такой постановке ответ почти очевиден. Кролик гарантированно встретится с хотя бы одной лисой, если любая прямая по которой он движется пересечёт хотя одну окружность Апполония. То есть имеет место следующая ситуация:

Рисунок сделан с учётом того, что скорости лис могут быть различные, различие в скоростях лис определяет различие в радиусах. Совокупность окружностей Апполония ограничивают замкнутую внутреннюю область в которой располагается кролик.

Чтобы сложилась такая ситуация необходимо какое-то соотношение между скоростями лис, кролика и расстояниями между ними. А для того, чтобы получить возможность что-либо считать нам нужен радиус окружности Апполония.