Статья: Автоматно-графовая формальная модель композитного документооборота

Таким образом, поведение участника документооборота может быть представлено в виде последовательности состояний документов. Совокупность всех состояний документов представляет конечное множество, которое полностью описывает все возможные сценарии поведения участников.

3.2. Модель связности поведенческих единиц на графах

Для построения графа модели документооборота предлагается использовать способ отображения документооборота графами, предложенный автором в работе [5]. Для задания множества вершин графа будем использовать множество возможных состояний документов . Ребра графа зададим с помощью множества действий Д. Установим это соответствие таким образом, чтобы выполнялись следующие правила:

– одной вершине графа соответствует один и только один элемент множества ;

– одному ребру графа соответствует один и только один элемент множества ;

– одному элементу множества соответствует одна и только одна вершина графа;

– одному элементу множества соответствует одно и только одно ребро графа.

Такое тождественное отображение множеств состояний в множество вершин и множества состояний в множество ребер e можно математически определить следующим образом: для любого справедливо утверждение и , где . То есть определяются две парных грамматики – первая грамматика для установления перевода Ф в v, вторая грамматика – для установления перевода Д в e.

Таким образом, связи между вершинами тождественно соответствуют связям состояний моделируемого документооборота. В графе документооборота вершины графа соединяют ребра в том и только в том случае, если соответствующие вершинам состояния связаны действием, соответствующим ребру, то есть .

Направленность ребер устанавливается таким образом, чтобы отображать логику последовательности смены состояний документооборота. Вершина является входящей вершиной для вершины через ребро в том и только в том случае, если состояние i сменяется на состояние после совершения действия . Таким образом, состояниям , сопоставляются вершины графа , и каждая пара вершин и соединена дугой , идущей от к в том и только в том случае, когда состояние является входным состоянием для .

3.3. Модель поведенческой единицы на автоматах

В предложенной автором автоматной модели документооборота [6] система представляется в виде детерминированного конечного автомата. Автомат, представляющий поведенческую единицу документооборота задается общепринятой нотацией конечного автомата. В соответствии с ней автомат представляется следующим образом:

,

где – конечное множество состояний документов, которое тождественно множеству {}, что следует из определения композитного документооборота;

– конечное множество входных символов, образующих входной алфавит и представляющих собой данные, которые поступают на вход системы документооборота;

– функция переходов, аргументами которой являются текущее состояние и входной символ, а значением – новое состояние;

– начальное состояние (или множество начальных состояний докуемнтов) из множества ;

– множество заключительных, или допускающих состояний из множества .

Множество состояний автоматов {Q} получается из множества состояний документов. Завершающие состояния выделяются из общего множества состояний путем анализа каждого из состояний. Если при анализе выявляется состояние, которое имеет одну или несколько входящих связей, но не имеет ни одной исходящей, то оно помечается как завершающее. Состояния моделирующего автомата упорядочиваются таким образом, чтобы документооборот был представлен состояниями документа в порядке от начального состояния документа к завершающему.

Автомат исполняет функции переходов для принятия решения о выборе следующего состояния. Функции переходов программируются с помощью анализа действий участников документооборота. Производимое действие определяет результирующее состояние, для которого входными данными для определения выбора являются текущее состояние документа и участник процесса. Автомат реализует документооборот, в котором на каждом шаге происходит действие на основании процесса, и на основании анализа текущего состояния документа (исполнителя) принимается решение о следующем состоянии документа. Функция перехода автоматной модели является i-м элементом множества действий {Д} документооборота, после выполнения которого происходит смена состояния на состояние .

В реализованной автоматной модели документооборота в качестве алфавита автомата использован список участников. Символами алфавита обозначены ролевые участники производственных сценариев. Из этих символов образуются последовательности, обрабатываемые автоматом формальной модели. Последовательности символов, которые обрабатываются автоматом документооборота, являются допустимыми для модели. Такие последовательности символов приводят к корректному выполнению процесса документооборота и получению конечного результирующего документа. Последовательности символов, которые не принимаются автоматом, реализующим модель документооборота, являются недопустимыми для моделируемого процесса. Последовательности символов, принимаемые автоматом модели документооборота, являются его языком. Слова в этом языке являются возможными последовательностями участников документооборота, участвующих в процессе работы над документами.

Программирование автомата осуществляется путем установления соответствия между нотацией конечного автомата и композитного документооборота. То есть, после проведения декомпозиции процессов и синтеза модели {У, Д, Ф} строится автоматная модель документооборота, которая определяется пятеркой (A, S, , T, F), где {{A}≡ {У}, {S}≡ {Ф}, =,{S}≡ {}, {F}≡ {Д}}. При этом на каждом шаге автомата, множества соответствуют множествам, описывающим жизненный цикл модели документооборота. На каждом шаге существует соответствие и : {(=),(=),=,=}.

3.4. Иерархический конечный автомат

Для представления иерархического конечного автомата документооборота будем использовать описание ИКА из работы [9]. В соответствии с этим описанием ИКА представляется пятеркой (I, O, S, T, r), где I и O описывают множества входных и выходных алфавитов, S представляет множество состояний, функции переходов , r задает начальное состояние. Детерминированный ИКА может быть представлен шестеркой (I, O, S, , r), где описывает выходную функцию, описывает функции переходов.

О данной паре входных и выходных последовательностей , где и говорят, что она принимается ИКА T=(I, O, S, T, r), если существует последовательность состояний такая, что для всех j=0,…,t-1 и .

В настоящей статье будем рассматривать поведение ИКА, определенного отношением элементов входа и выхода. Иными словами, отношение между алфавитами входа и выхода есть набор пар входов и выходов, которые определяют состояния детерминированного ИКА. Для заданного автомата T=(I, O, S, T, r) поведение между входом I и выходом O содержится в функциях переходов T, если каждая пара последовательности входов и выходов реализуется в T. Рассмотрим реализацию ИКА, управляющего конечными автоматами на примере на рис. 1.

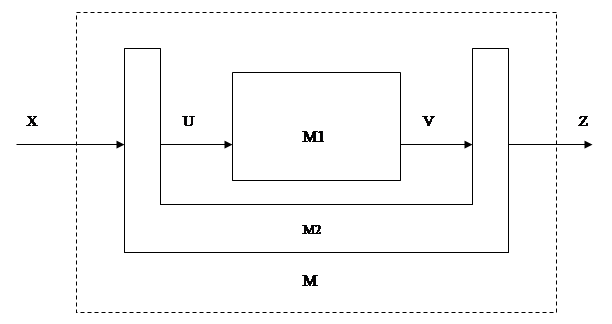
Рисунок 1. Пример иерархического конечного автомата.

Итак, заданные автоматы M=(I, O, S, ,r) и M2 = (). Предполагается, что система документооборота может принимать сразу несколько состояний, в то время как один исполнитель производит смену состояния только на одно из возможных. Таким образом, автомат M может быть НДКА, в то время, как автомат M2 может быть только ДКА. Выходная функция автомата M2 состоит из , которые соответственно определяются выходными функциями U и Z.

Заданы подмножество из множества состояний S и вход x автомата M, зададим как множества всех возможных выходов. То есть в том и только том случае, если существует такое, что . Аналогично, будет множеством всех возможных состояний, то есть в том и только том случае, если такое, что .