Статья: Автоматно-графовая формальная модель композитного документооборота
При заданном автомате ![]() детерминированный конечный автомат
детерминированный конечный автомат ![]() считается реализуемым на M1, если существует хотя бы одна пара цикличных реализаций M1 и M2, таких, что их соединение не вызывает цикла между U и V.
считается реализуемым на M1, если существует хотя бы одна пара цикличных реализаций M1 и M2, таких, что их соединение не вызывает цикла между U и V.
При заданных автоматах![]() и
и ![]() ДКА
ДКА ![]() является допустимым автоматом, если автомат M1 реализуем и поведение
является допустимым автоматом, если автомат M1 реализуем и поведение ![]() содержится в M, где
содержится в M, где ![]() является выходным результатом M. Поведение, которое реализуется допустимым автоматом, является допустимым поведением.
является выходным результатом M. Поведение, которое реализуется допустимым автоматом, является допустимым поведением.
3.4.1. Свойства ИКА
Рассмотрим применение НДКА для реализации ИКА. Пусть при данном ![]() надо получить
надо получить ![]() и
и ![]() для заданного
для заданного ![]() , где
, где ![]() означает мощность множества S. Пусть при этом
означает мощность множества S. Пусть при этом ![]() и
и ![]() являются подмножествами
являются подмножествами ![]() , а
, а ![]() и
и![]() . Функция перехода существует, т.е
. Функция перехода существует, т.е ![]() , если выполняются три следующих условия:
, если выполняются три следующих условия:
1) ![]() ;
;
2) ![]() ;
;
3) 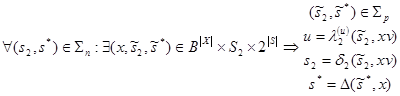 .
.
В каждом из вычислений ![]() есть множеством подмножества
есть множеством подмножества ![]() . Причем пустое подмножество {0} тоже может входить во множество
. Причем пустое подмножество {0} тоже может входить во множество ![]() . При заданном
. При заданном ![]() множество
множество ![]() вычисляется следующим образом:
вычисляется следующим образом: ![]() в том и только том случае, если также
в том и только том случае, если также ![]() или
или ![]() .
.
Пусть K будет позитивным целым, таким, что ![]() . Такое K всегда существует, если количество элементов множества
. Такое K всегда существует, если количество элементов множества ![]() не возрастает во время вычислений и количество подмножеств
не возрастает во время вычислений и количество подмножеств ![]() конечно.
конечно.
Пусть ![]() будет такой связью, что
будет такой связью, что ![]() в том и только в том случае, если
в том и только в том случае, если ![]() или
или ![]() .
.
Значит, мы можем определить ИКА документооборота пятеркой![]() , где
, где ![]() . При этом каждое состояние ИКА представляет подмножество
. При этом каждое состояние ИКА представляет подмножество![]() .
.
3.4.2. Архитектура ИКА
В работе [10] показано, что рекурсивные алгоритмы могут быть построены из иерархических модулей, которые вызывают сами себя и рекурсивно передают входные и выходные данные. На рисунке 2 показана рекурсивная функция gcd. Локальные состояния x1 и x2 определяют соответствующую ветвь алгоритма. Микрооперации y1 и y2 осуществляют обработку данных и рекурсивную передачу данных между модулями алгоритма. Рекурсия организуется путем многократного вызова одного модуля, в нашем случае модуля Z.


Рис. 2. Рекурсивная функция gcd
Архитектура иерархического конечного автомата, который может рекурсивно обрабатывать конечные автоматы, приведена на рис. 3.


Рис. 3. Архитектура ИКА.
Иерархический КА, который приведен на рис. 3, имеет два технологических стека. Один стек автомата, который обозначен FSM_stack, предназначен для обработки состояний. Второй стек, обозначенный M_stack, предназначен для обработки модулей, представляющих собой автоматы моделирования поведенческих единиц.
Взаимодействие стеков обеспечивается синхронизационным модулем. Синхронизационный модуль отвечает за вызов новых модулей, передачу входных состояний активизированному модулю и получение выходных состояний из модуля, который заканчивает работу.
Состояние внутри ИКА соответствует состояниям a0…a4 на рис. 1. Поскольку каждый конкретный модуль имеет уникальный идентификатор, то обозначения одних и тех же состояний могут использоваться в различных модулях. На рис. 2 показано, как ИКА исполняет алгоритм, приведенный на рис. 1.
Все неиерархические вызовы производятся путем смены кода модуля в верхнем состоянии регистра FSM_Stack. На рис. 2 такой пример обозначен знаком «*». Все иерархические вызовы изменяют состояния обоих стеков. При этом M_Stack сохраняет код нового модуля, а FSM_Stack устанавливается в начальное состояние инициализируемого модуля. Такой пример на рисунке 2 обозначен символом «#».
Иерархический вызов активирует операцию «pop» без изменения стеков, на рисунке это обозначено «&». В результате завершения работы модуля ИКА перейдет в состояние, последующее за состоянием, на котором был произведен вызов модуля. Указатель стеков stack_ptr является общим для обоих стеков. Работа ИКА прекращается при достижении позиции «End» и состоянии указателя stack_ptr =0.
Таким образом, работают описанные выше автоматы, составляющие автоматную часть формальной модели композитного документооборота.
5. Выводы
Представление модели документооборота в виде ИКА позволяет применить к задачам документооборота апробированный аппарат. В результате сложные процессы документооборота могут быть формально представлены в виде единого автомата, которые в свою очередь оперирует автоматами, а каждый из них моделирует единицу поведения системы. Каждый из автоматов моделирует поведение участника, обрабатывающего изменения состояний документов.
Последовательность обработки автоматов центральным автоматом определяется связями, описанными графом, который устанавливает связность автоматов между собой. Применение графов позволяет использовать апробированный и развитый аппарат теории графов при описании связности обрабатываемый автоматов.
Такое представление дало возможность реализовать двигатель управленческих процессов, основанный на формальных моделях. Этот двигатель является центральной частью программного реализованного комплекса композитного документооборота.
ЛИТЕРАТУРА
- Теслер Г.С. Новая кибернетика.- Киев: Логос, 2004. – 401с.
- Алферова З.В. Математическое обеспечение экономических расчетов с использованием теории графов.-М: Статистика.- 1974. – 208с
- Clarence Ellis Team Automata for Groupware Systems. - Arizona:ACM SIGGROUP., 2001, P.415-424
- Marc Hoffman, David Shute, Mike Ebbers Advanced Workflow Solutions. -New York: Redbooks IBM, 1999.- 141 p.
- Круковский М.Ю. Графовая модель композитного документооборота// Математичні машини і системи. – 2005. – № 3. – С. 149 – 163.
- Круковский М.Ю. Автоматная модель композитного документооборота Математичні машини і системи.-2004.-№4.-С.37-50.
- Inout Cardei, Rakesh Jha, Mihaela Cardei Hierarchical architecture for real-time adaptive resource management. – Secaucus, NJ, USA: Springer-Verlag.- 2000.-434p.
- Круковский М.Ю. Методология построения композитных систем документооборота // Математичні машини і системи. – 2004. – № 1. – С. 101 – 114.
- Yosinori Watanabe, Robert Brayton. The maximum set of permissible behaviors of FSM networks.-Los Alamitos CA USA// IEEE Computer society press.-1993.-pp.316-420
- Valery Sklyarov. Hardware implementation of hierarchical FSMs.- Cape Town, South Africa: ACM, 2005.-p. 148-153