Статья: «Безвихревая электродинамика». Математическая модель
![]() .
.


![]()

![]()
![]()
![]()
![]()
![]()
Возвращаясь к равенству (1) отметим, что его правая сторона совпадает с
уравнением из таблицы1. Частичную инвариантность этого скалярного уравнения только по отношению к пространственным поворотам следует понимать в том смысле, что оно «извлечено изнутри» полностью инвариантного максвелловского.
Плоская поперечно-векторная ЭМВ занимает в 4-мерном пространстве-времени две взаимно ортогональные пространственные координаты. Свободными для полевых компонент общей ЭМВ остаются одна пространственная (продольная) и временная (скалярная) координаты, которые они и занимают сохранившимися скалярными модулями, и новыми продольными векторами.
Наглядным образом скалярных компонент уравнений безвихревой электродинамики являются соответствующие векторные диаграммы нуль-векторов. Знак скаляра предлага-
ется положительным для расходящихся противонаправленных векторов, отрицательным – для сходящихся.
Сопоставление 3-мерных компонент основополагающих уравнений двух электродинамикчески представлены в таблице 2.
Таблица 2
| Компоненты уравнений безвихревой электродинамики | Компоненты уравнений вихревой электродинамики |
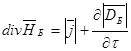 | |
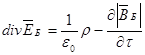 | |
‡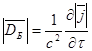 | ‡ |
| ‡ | ‡ |
| ‡ | |
| ‡ | ‡ |
 | |
| ‡ | ‡ |
| ‡ | ‡ |
Электромеханическая связь. Для вывода электромеханической связи образуем две пары 3 – мерных уравнений
![]() , (30)
, (30)
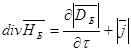 (31)
(31)
и
![]() , (32)
, (32)
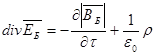 . (33)
. (33)
Просуммируем их попарно, предварительно умножив каждое соответственно на ![]() ,
,
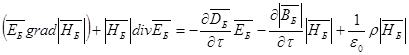 . (34)
. (34)
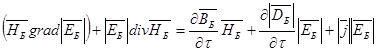 , (35)
, (35)
Используя формулу векторного анализа
![]() , (36)
, (36)
в итоге получим