Статья: Фазовая, групповая и сверхсветовая скорости
Критически проанализированы понятия фазовой и групповой скоростей в дисперсной среде. На основании проведенного анализа был сделан вывод о неправомерности введения понятия “групповая скорость”. Также был сделан вывод, что модулирующий сигнал (импульс) в дисперсных средах распостраняется с фазовой скоростью несущей волны, а дисперсность среды проявляется только в уширении сигнала. Данное положение проиллюстрировано расчетом параметров линии при высокой дисперсности среды. Сделан вывод о возможности передачи сигнала и энергии со сверхсветовыми скоростями.
1. Немного истории.
Вначале прошу меня извенить за цитированеие:
“В классической механике Ньютона описание взаимодействия тел с помощью потенциальной энергии предполагает мгновенное распостранение взаимодействий. В действительности (?? Г. И.) существует максимальная конечная скорость С распостранения взаимодействия (?? Г. И.), причем в природе невозможно взаимодействие со скоростью, превышающей С (?? Г. И.). Максимальная скорость распостранения взаимодействий является универсальной постоянной (?? Г. И), одинаковой во всех инерциальных системах (?? Г. И.); она равна скорости распостранения света в вакууме (?? Г. И.)..... Соединене принципа относительности с утверждением о конечности максимальной скорости распостраненя взаимодействий называется специальным принципом относительности Эйнштейна” , Б.М.Яворский, А.А. Детлаф “Справочник по физике” стр. 480 (выделено Г. И.).
Совершенно очевидно, что ВСЕ эти положения являются допущениями (волюнтаристскими утверждениями) – т.е. постулатами.
Таким образом, в начале 20-го века Эйнштейн ввел в свою СТО ряд постулатов, в частности постулат о невозможности скоростей, превышающих скорость света в вакууме (которая также постулировалсь как мировая константа) и о постоянстве скорости света во всех системах координат. Согласно последнему, скорость света не складывалась не только со скоростью источника излучения, но и, в отличии от скорости звука в акустике, со скоростью приемника излучения. Для подтверждения этого “постулата” были использованы результаты экспериментов с механической модуляцией света и с прохождением света в средах, которые .были проведенны в 19-м веке на соответствующем оборудовании (Физо, Араго и проч.). Критический анализ этих экспериментов выходит за рамки данной статьи, хотя, надо заметить, что все они, в частности “водяные эксперименты” Физо, вызывают большие сомнения в корректности их интерпретации (теория электромагнитных волн была разработана позднее), а точности измерений соответствовала технике 19 века.
В начале 20-го века были проведены некие дополнительные эксперименты, направленные уже на “нахождение эффектов второго порядка, подтверждающих СТО”, в частности, эксперимент Айвена (описание которого кочует из учебника в учебник) по нахождению поперечного эффекта Доплера. Все эти “эксперименты по подтверждению”, конечно же с высокой точностью совпали с предсказанием СТО, так как были заранее запрограммированы на “нахождение” необходимых эффектов. Другие же эффекты, являющиеся очевидным следствием сложения скорости света со скоростью приемника (как в акустике), такие, например, как “звездная аберрация”, эффект Саньяка и фотон-фононное взаимодействие в акусто-оптике, в расчет не принимались (правда, последний был открыт только в 60-х годах). Но, так как их существование нельзя было отрицать (эффекты, отнюдь, не “второго порядка малости”), то релятивисты вынуждены были дать им объяснение. Например эффект Саньяка (лазерные гироскопы) объяснялся с помощью ОТО (?!), как “искривление пространства” при вращении гироскопа (?!).
Далее, кто-то вдруг вспомнил об аномальной дисперсии, открытой еще в середине 19-го века (Эйнштейн, по видимому, о ней просто не знал). Известно, что вблизи полос поглощения происходит разрыв зависимости коэффициента преломления от длины волны, напоминающий функцию тангенса. При этом, в области, короче длины волны поглощения, наблюдается уменьшение коэффициента, а в области, выше длины волны поглощения – его возрастание (Рис. 1).
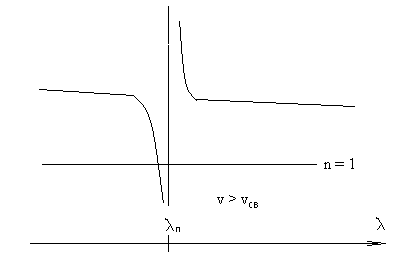
Рис. 1
В ранних измерениях этого эффекта использовались спектрометры со слабым разрешением и относительно высокотемпературные среды, в следствии чего эффект “смазывался”. Но с возрастанием точности спектрометров, а, также при захолаживании среды, обнаружилось, что коэффициент преломления в первой области становится меньше единицы! А ведь это значит, что скорость света в данной среде выше скорости света в вакууме! Но, ведь это является ересью и подрывает “основы мироздания”, то есть “великую и бесспорную СТО”! Тут релятивисты засуетились и стали что-то срочно придумывать. И тут они вспомнили английского ученого Рэлея, “выяснившего сложный характер понятия скорости волны” и введшего понятия “групповой и фазовой” скоростей.
Под “фазовой скоростью” Рэлей подразумевал собственно скорость распостранения монохроматической волны, а вот под “групповой скоростью” – некую скорость распостранения гармоник, представляющих импульс и, даже не гармоник, а некой характерной точки импульса. Далее утверждалось, что только совокупность этих скоростей и определяет скоростью распостранения волны – то есть скоростью распостранения энергии и некой информации (в ТО философское понятие “скорости распостранения взаимодействия и информации” является очень важным и на ней построена вся “эйнштейнова философия”).
2. Фазовая и групповая скорости
Для выяснения природы этих скоростей представляется необходимым подробно рассмотеть последовательность вывода этих скоростей, приведенных, например, в университетском учебнике Г. С. Ландсберга “Оптика” [1] на стр. 428. Надо отметить, что в этом выводе приводится много общефилософских утверждений, которые автор данной статьи считает весьма спорными, и которые часто напоминают апорию Зенона об Ахиллесе и черепахе.
Начинается же вывод с философского утверждения, что “понятие фазовой скорсти применимо только к сторого монохроматическим волнам, которые реально не осуществимы, так как они должны были бы существовать неограниченно долго во времени и быть бесконечно протяженными в пространстве”, то есть принципиально не существует источника излучения, излучающего вечно. Здесь, по видимому, имеется в виду, что излучения с бесконечно длинным импульсом не бывает. Тут автор книги [1] забывает об обычной радиолампе (имеется в виду радиопередатчик с антенной), которая теоретически может излучать монохроматическую поляризованную электромагнитную волну сколь угодно долго. Далее продолжается: “В действительности мы всегда имеем более или менее сложный импульс, ограниченный во времени и пространстве”. Надо отметить, что эти высказывания вполне достойны Зенона. Очевидно, что бесконечного во времени и пространстве не бывает ничего, но бывает сколь угодно к этому приближенное!
Далее по тексту книги [1] приводится математический вывод, который должен проиллюстрировать наличие “групповой скорости”.
Вывод сразу начинается с принципиально неправильного положения, что две волны с близкими параметрами определяют некий импульс: “Для простоты вычисления мы будем представлять себе импульс как совокупность двух близких по частоте синусоид одинаковой амплитуды...”. Тут надо сразу же отметить, что в случае ЛЮБОЙ модуляции возникают, как минимум, ТРИ волны, несущая – с угловой частотой ω, первая боковая – с угловой частотой ![]() и вторая боковая
и вторая боковая ![]() , (см. стр. 34 – 35 этой же книги) и модулированный сигнал определяется сложением этих ТРЕХ частот. Как правильно написано на стр. 34 той же книги [1], “...наша волна есть ничто иное, как совокупность трех строго монохроматических волн с амплитудами А, Ѕ A, ½ A и частотами n, n + m, n – m. Совокупность этих трех монохроматических волн и составляет заданную немонохроматическую волну.”. Кроме того, совершенно очевидно, что каждая из этих волн переносят свою порцию энергии (мощности). Случай же биений ДВУХ частот к передаче импульса не имеет никакого отношения.
, (см. стр. 34 – 35 этой же книги) и модулированный сигнал определяется сложением этих ТРЕХ частот. Как правильно написано на стр. 34 той же книги [1], “...наша волна есть ничто иное, как совокупность трех строго монохроматических волн с амплитудами А, Ѕ A, ½ A и частотами n, n + m, n – m. Совокупность этих трех монохроматических волн и составляет заданную немонохроматическую волну.”. Кроме того, совершенно очевидно, что каждая из этих волн переносят свою порцию энергии (мощности). Случай же биений ДВУХ частот к передаче импульса не имеет никакого отношения.
Если же модулирующий импульс имеет сложную форму, например, прямоугольную, его спектр содержит больше гармоник (гармоники модулирующего сигнала, не несущей!), каждая из которых модулирует несущую волну и представлена двумя боковыми частотами и, соответственно, сигнал образуется сложением всех боковых с несущим сигналом. Кроме того, не надо забывать, что в пространстве эти волны движутся независимо, не взаимодействуя друг с другом, а складываются (интерферируют) только на приемнике. Кстати, на стр. 33 книги [1], опять же, правильно написано, что “Практически весьма хорошее приближение (к исходной форме импульса, Г. И.) получается обычно, если ограничиться небльшим числом членов ряда Фурье”. Известно, например, что при воспроизведении прямоугольного импульса можно ограничиться 3-й гармоникой. В то же время, автор книги [1], видимо считая, что студенты забыли, то, что написано на стр. 33, на стр. 428 книги пишет: “..мы можем представить импульс как наложение бесконечно большого числа близких по частоте монохроматических волн (представление импульса в виде интеграла Фурье)”. Математически это, естественно, правильно, но совершенно не подходит к рассматриваемому случаю (см. выше). В дальнейшем автор, как бы вбивая гвоздь, несколько раз повторяет, что “Группой волн называют импульс, который можно представить в виде совокупности бесконечного числа синусоид, частота которых мало отличается друг от друга.”. Напрашивается вопрос, зачем надо вводить эту “бесконечную” абстракцию? Очевидно, автор понимал особую важность “групповой скорости”, а под это “понятие” надо было подвести философскую “базу”. Кстати, нынешние “опровергатели сверхсветовых скоростей” слово в слово повторяют эти “доводы”. Кроме того, интеграл Фурье, так часто упоминаемый в книге [1], не имеет никакого отношения к модуляции сигнала синусоидальным сигналом (там, как было уже сказано, присутствуют только три волны и без всякого “бесконечного количества волн с бесконечно малой амплитудой”).
Затем Ландсберг переходит непосредственно к доказательству существования групповая скорости, отличающейся от скорости любой составляюшей этого “волнового пакета”.
На стр. 429 он рассматривает случай сложения ДВУХ волн, при котором, как уже было указано выше, образует биения, не имеющие никакого отношения к передаче импульса (информации). Очевидно, что узлы этих биений НЕ ЯВЛЯЮТСЯ ИМПУЛЬСАМИ, и выделение неких точек на биениях и нахождение “скорости их перемещения” является совершенно не правомерным!
Для определения же истинного характера прохождения модулирующего сигнала в дисперсной среде необходимо рассмотреть случай модуляции монохроматической волны, например, синусоидальным сигналом.
В этом простейшем случае, когда модуляция осуществляется синусоидальным сигналом, мы имеем три волны:
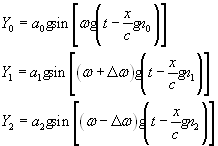
где ![]() ,
, ![]() ,
, ![]() - амплитуды,
- амплитуды, ![]() ,
, ![]() ,
, ![]() - коэффициенты преломления (дисперсной среды) ни частотах
- коэффициенты преломления (дисперсной среды) ни частотах ![]() ,
, ![]() ,
, ![]() . Здесь надо помнить, что практичеси всегда Δω<<ω и глубина модуляции <100%, то есть
. Здесь надо помнить, что практичеси всегда Δω<<ω и глубина модуляции <100%, то есть ![]() .
.
Можно, конечно, вспоминая курс средней школы, сложить три синуса, получив при этом аналитическое выражение для огибающей модулирующего сигнала. Намного же проще и наглядней сложить эти синусоиды графически (см. рис. 2).
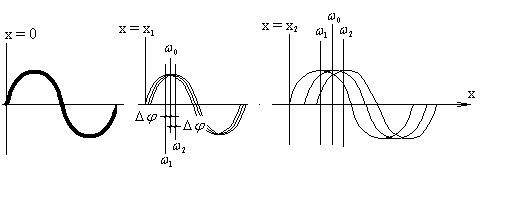
Рис. 2
Здесь на первом графике представлен сигнал (синусоидальная несущая волна, модулированная синусоидальным сигналом малой частоты, то есть ![]() ) на выходе из передатчика (при Х = 0). На втором и третьем графиках представлено положение волн на расстояниях
) на выходе из передатчика (при Х = 0). На втором и третьем графиках представлено положение волн на расстояниях ![]() и
и ![]() от передатчика.
от передатчика.
Очевидно, что при х = 0 все три волны совпадают по фазе. Далее они начинают “расходиться”. Это значит, что первая боковая, для которой ![]() начинает отставать по фазе от несущей, а вторая боковая, для которой
начинает отставать по фазе от несущей, а вторая боковая, для которой ![]() – опережать.
– опережать.
Фазовый сдвиг боковой относительно несущей может быть определен по формуле:
![]() , где
, где ![]() – угловая частота несущей,
– угловая частота несущей, ![]() - угловая частота модуляции (
- угловая частота модуляции (![]() ), х – расстояние, пройденное сигналом (длина линии), с – скорость света в вакууме,
), х – расстояние, пройденное сигналом (длина линии), с – скорость света в вакууме, ![]() - производная зависимости коэффициента преломления от частоты
- производная зависимости коэффициента преломления от частоты ![]() . При этом считалось, что
. При этом считалось, что ![]() . Таким образом, происходит “фазовое уширение сигнала” равное
. Таким образом, происходит “фазовое уширение сигнала” равное ![]() (при линейной зависимости
(при линейной зависимости ![]() ). При дальнейшем уширении импулса он полностью деформируется (распадается) и при фазовом сдвиге, равном 2π, форма сигнала (синусоидального) будет повторена. Если “выделить” центр импульса (чем не характерная точка!), то совершенно очевидно, что скорость распостранения сигнала будет равна ФАЗОВОЙ СКОРОСТИ НЕСУЩЕЙ ВОЛНЫ! Очевидно также, что ПОНЯТИЯ “ГРУППОВОЙ СКОРОСТИ” НЕ СУЩЕСТВУЕТ! Существует только “уширение сигнала”, которое и ограничивает скорость предачи данных и длину линии в дисперсной среде.
). При дальнейшем уширении импулса он полностью деформируется (распадается) и при фазовом сдвиге, равном 2π, форма сигнала (синусоидального) будет повторена. Если “выделить” центр импульса (чем не характерная точка!), то совершенно очевидно, что скорость распостранения сигнала будет равна ФАЗОВОЙ СКОРОСТИ НЕСУЩЕЙ ВОЛНЫ! Очевидно также, что ПОНЯТИЯ “ГРУППОВОЙ СКОРОСТИ” НЕ СУЩЕСТВУЕТ! Существует только “уширение сигнала”, которое и ограничивает скорость предачи данных и длину линии в дисперсной среде.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--