Статья: Исследование одной модели газотранспортной сети

В статье рассматривается одна из моделей газотранспортной сети на основе объектного подхода. Отражена постановка задачи, математические модели ее элементов (труб, подкачек, отборов, компрессорных станций), а также правила взаимодействия элементов между собой. Представлен алгоритм расчета временного слоя всей сети. В заключении освещены результаты тестирования этой модели, реализованной на компьютере.

Введение

Газотранспортные сети (ГТС) являются важным и сложным объектом изучения, т.к. являются носителем одной из гибких форм энергоносителя (газа). Соответственно моделирование, расчет и оптимизация режимов работы ГТС вызывает большой интерес как у исследователей, так и пользователей подобных систем. Существует много моделей созданных по данной тематике. Отличительной чертой рассматриваемой модели является гибкость построения сложных систем ГТС

В данной работе рассматривается только математическая модель и расчет ГТС. Оптимизация на основе этой модели выходит за рамки статьи. Общая модель ГТС включает уже изученные модели ее элементов (труб, подкачек, отборов, КС). Необходимо отметить, что данная модель разрабатывалась с возможностью добавления в дальнейшем модулей оптимизации по заданным критериям.

Определим задачу, которую должна описывать и решать модель ГТС. Пусть заданы начальное распределение давления P_i,0 по всей ГТС (где i=1,..,n v пространственный слой) и граничные условия на подаче и отборе газа в систему по времени. Необходимо определить распределение давления P_i,j и расхода Q_i,j по ГТС для каждого временного слоя j, где j=1,...,m. Пример ГТС с элементами приведен на рис.1

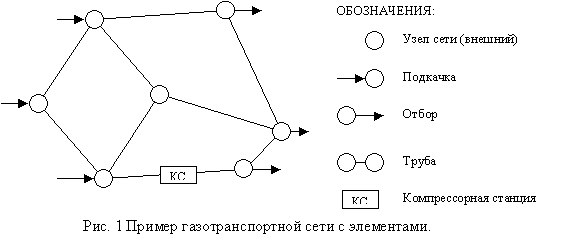
В основе данного подхода к построению модели ГТС лежит предположение, что сеть состоит из ряда объектов, взаимодействующих между собой по определенным алгоритмам. Для сети это два класса объектов v узлы и ребра, которые и представляют собственно сеть. На основе элементов этих классов строится сеть необходимой сложности. Основное отличие классов в том, что каждое ребро может быть связано не более чем с двумя узлами, а узел в свою очередь не имеет ограничений по количеству, относящихся к нему ребер.

Класс узлов состоит из следующих типов объектов:

узлы между ребрами (внешние)

узлы по длине трубы, т.е. внутренние узлы ребра.

Исходя из определения, внутренние узлы связаны с двумя соседними частями ребра. Так как вычисления по ним ведутся по математической. модели трубы, примем их как единое целое с объектом ?труба¦.

Класс ребер состоит из следующих типов объектов:

подкачки, т.е. объекты подачи газа в ГТС;

отборы, т.е. объекты отбора газа из ГТС;

трубы;

компрессорные станции (КС).

Рассмотрим каждый тип подробнее.

Подкачки осуществляют подачу газа в ГТС, имеют ссылку только на один узел ГТС (узел, куда осуществляется подача газа). По времени для них задается изменение давления P_i,j или расхода Q_i,j (граничные условия), где j=1,-,m - это количество временных слоев для расчетов.

Отборы осуществляют отбор газа из ГТС, имеют ссылку только на один узел ГТС (узел, куда осуществляется отбор газа). По времени для них также задается изменение давления P_i,j или расхода Q_i,j (граничные условия), где j=1,...,m - это количество временных слоев для расчетов.

Трубы осуществляют передачу газа по ГТС, имеют ссылку на два внешних узла ГТС (откуда идет поступление газа и откуда идет отбор газа из трубы). Для них задается начальное распределение давления газа P_i,0 в момент времени t₀ , где i=1,...,n v это количество внутренних узлов трубы.

КС осуществляют увеличение давления между двумя внешними узлами ГТС с сохранением массового расхода газа за счет увеличения потенциальной энергии газа. Другими словами, КС поддерживают по времени определенный массовый расход в определенном направлении. Для полной характеристики КС нам необходимо учитывать физические характеристики КС, затраты газа на внутренние нужды КС и др. Но для упрощения модели КС можно задавать только изменение расхода газа Q_0,j по времени, которое по сути будет содержать в себе все остальные параметры КС. Таким образом, КС имеют ссылку на два внешних узла ГТС (откуда идет поступление газа и откуда идет отбор газа из трубы) и для них задается изменение расхода газа Q_0,j по времени, где j=1,...,m - это количество временных слоев для расчетов.

Для всех ребер кроме труб изменение давления или расхода по времени задается. Поэтому основная сложность заключается в том, чтобы определить состояния труб и внешних узлов ГТС для каждого временного слоя.

Модель движения газа по трубе

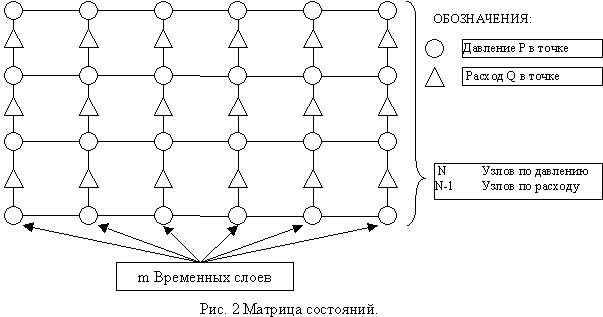
По начальному состоянию газа в трубе и краевым условиям на концах трубы необходимо определить конечное состояние газа на определенном временном слое. Параметрами состояния являются давление газа P_i,j и его расход Q_i,j в точке трубы. Все остальные физические параметры газа, трубы принимаются константами на текущий момент расчета. Тогда состояние трубы - это набор точек вдоль трубы (их количество n). Обычно расстояние между ними берут одинаковым (D X). Так как от начального до конечного состояния происходит какой-то промежуток времени T, его тоже можно разбить на m промежутков D t, чтобы можно было проследить изменение состояния в n точках трубы на каждом из m промежутков времени (или временных слоев). В итоге решение - это плоскость распределения давления и расхода по времени и длине трубы.

Приводим возможные варианты состояния газа в трубе:

Стационарное состояние газа (без движения). Когда давление газа одинаково по всей трубе P=const и соответственно расход газа Q=const.

Стационарное движение газа. Когда давление газа неодинаково распределено по всей трубе и рассчитывается по формуле стационарного режима, но расход газа Q=const по всей трубе.

Нестационарное движение газа. Когда давление газа P также неодинаково распределено по трубе, но при этом расход газа Q распределен по трубе также неодинаково.

Исходя из постановки задачи имеется начальное состояние трубы в виде массивов P_i,0 и Q_i,0 (где i=1,.,n). Тогда совокупность всех временных слоев (т.е. состояний на текущий момент) описывается состоянием труб P_i,j и Q_i,j (где i=1,....,n и j=1,...,m).

Для вычислений состояний газа при нестационарном его движении из теории газовой динамики применяют следующую систему нелинейных дифференциальных уравнений [1]:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--