Статья: Кривые, заданные в полярных координатах
Р.Л. Ткачук
Вологда
Введение
Тема «Полярная система координат» позволяет познакомить учащихся с красивейшими результатами математической науки.
Полярная система координат на плоскости определяется заданием точки O(полюс), луча Ох (полярная ось) и единичного отрезка т. Кроме того, должен быть указан поворот луча Ох, называемый положительным. Пусть это будет поворот в направлении против движения часовой стрелки. Повороты луча, совершаемые в направлении, противоположном положительному, будем называть отрицательными.
Пусть М — произвольная точка плоскости, не совпадающая с полюсом. Обозначим через ![]() длину отрезка ОМ, а через
длину отрезка ОМ, а через ![]() — величину угла, образованного лучами Ох и ОМ. Числа
— величину угла, образованного лучами Ох и ОМ. Числа ![]() и
и ![]() такие, что р>0 и 0
такие, что р>0 и 0 ![]() ф < 2π, именуют полярными координатами точки М. Число
ф < 2π, именуют полярными координатами точки М. Число ![]() называют первой полярной координатой, или полярным радиусом, число
называют первой полярной координатой, или полярным радиусом, число ![]() — второй полярной координатой, или полярным углом (рис. 1) Если точка М совпадает с полюсом, то
— второй полярной координатой, или полярным углом (рис. 1) Если точка М совпадает с полюсом, то ![]() = 0, а полярный утол
= 0, а полярный утол ![]() считаем равным нулю. Заметим, что при заданных нами условиях
считаем равным нулю. Заметим, что при заданных нами условиях ![]() > 0, 0 ≤
> 0, 0 ≤![]() < 2π, полярные координаты любой точки определяются однозначно.
< 2π, полярные координаты любой точки определяются однозначно.
Введение таких координат очень естественно, ведь местонахождение любой точки на земной поверхности для неподвижного наблюдателя удобно определять с помощью расстояния от наблюдателя до этой точки и направления к точке от наблюдателя (в этом случае точка, в которой находится наблюдатель, служит полюсом).
Школьникам можно напомнить, что в повести Р.Л.Стивенсона «Остров сокровищ» описано, как старый пират Флинт определил местоположение закопанного клада: «Десять футов к северу от высокого дерева на склоне Подзорной Трубы» (рис. 2).
Построение кривых, заданных полярными уравнениями, имеет некоторые специфические особенности, которые мы проиллюстрируем на примерах. Как известно, математики Древней Индии заменяли доказательства теорем геометрическим чертежом, сопровождая его короткой подписью: «Смотри!». Мы пользовались тем же принципом, заменив долгие разъяснения рисунками, из которых видны все свойства кривых.
В дальнейшем, при построении кривых мы позволим углу ![]() принимать любые неотрицательные значения, выделяя на рисунках жирной линией фрагменты кривых, получающиеся при ограниче-нии 0 ≤
принимать любые неотрицательные значения, выделяя на рисунках жирной линией фрагменты кривых, получающиеся при ограниче-нии 0 ≤![]() < 2π.
< 2π.
Алгебраические спирали
Сначала рассмотрим так называемые алгебраические спирали, т.е. кривые, полярные уравнения которых являются алгебраическими относительно ![]() и
и ![]() и имеют вид F(
и имеют вид F(![]() ,
,![]() ) = 0,
) = 0, ![]() ≥0,
≥0, ![]() ≥ 0. Если перейти к прямоугольной системе координат, то эти уравнения уже не будут алгебраическими относительно х и у. Кривые, задаваемые такими уравнениями, принято называть трансцендентными.
≥ 0. Если перейти к прямоугольной системе координат, то эти уравнения уже не будут алгебраическими относительно х и у. Кривые, задаваемые такими уравнениями, принято называть трансцендентными.
Достаточно громоздкие декартовы уравнения упрощаются при переходе к полярной системе координат. Зависимость между полярными и декартовыми координатами весьма проста.
Пусть полюс Oсовпадает с началом декартовой системы координат, полярная ось совмещена с положительным направлением оси Ох; М(х; у) — произвольная точка декартовой плоскости. Легко убедиться, что
![]()
И обратно:
x=![]()
Спираль Архимеда
![]() =
= ![]() .
.
Поместим точку на секундную стрелку часов и будем перемешать точку вдоль секундной стрелки с постоянной скоростью, не обращая внимания на равномерное движение стрелки часов по кругу. Тогда точка опишет кривую, называемую спиралью Архимеда. Изобретение этой кривой приписывается Конону Самосскому, хотя ее основные свойства описал именно Архимед (ок. 287-212 гг. до н.э.). Архимеду, в частности, было известно, что расстояние между двумя последовательными витками спирали является постоянной величиной и равно 2π (рис. 3).
Кстати, в силу этой особенности в расположении витков реальный образ спирали Архимеда можно видеть, например, наблюдая туго завернутый рулон бумаги с его торцевой стороны.
На внеклассных занятиях полезно показать построение первого витка спирали Архимеда.
Начертим окружность. Разделим ее и радиус ОА на п равных частей.
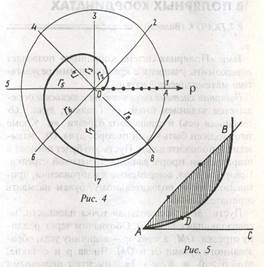
Пусть n = 8. Проведем ко всем точкам деления лучи из центра О окружности и пронумеруем их (рис. 4). На луче 1 отметим точку на расстоянии![]() =
=![]() ОА от центра окружности. На луче 2 отметим точку на расстоянии
ОА от центра окружности. На луче 2 отметим точку на расстоянии ![]() =
=![]() ОА, на луче 3 - точку на расстоянии
ОА, на луче 3 - точку на расстоянии ![]() =
=![]() ОА и т.д. На луче 8 поставим точку на расстоянии
ОА и т.д. На луче 8 поставим точку на расстоянии ![]() =
=![]() ОА.
ОА.
Соединив последовательно плавной кривой полученные точки, мы увидим первый виток спирали Архимеда. Построение будет тем более точным, чем больше точек деления радиуса и окружности будет выбрано первоначально.
Спираль Архимеда используется в качестве линии, позволяющей разделить заданный угол на любое количество равных частей. В некоторых готовальнях в старину в состав рабочих инструментов входила металлическая пластинка с тщательно выгравированной на ней спиралью Архимеда. С помощью такого приспособления было нетрудно разделить угол на несколько равных частей. Например, для трисекции угла ВАС достаточно приложить пластину ее ровной частью к одному из лучей угла (рис. 5) и поделить получившийся отрезок АВ на 3 равные части. На дуге спирали следует сделать засечку радиусом АО = - АВ. Тогда угол САО будет равен одной трети угла ВАС.
В области техники спираль Архимеда находит применение в так называемых кулачковых механиз-мах, которые преобразуют вращательное движение шайбы в поступательное движение стержня. В некоторых механизмах (например, в часах) требуется, чтобы стержень двигался равномерно. Обеспечить это можно, очертив профиль шестеренки по спирали Архимеда.
В качестве второго объекта для применения спирали Архимеда в технике можно привести самоцентрирующийся патрон (рис. 6), направляющие канавки которого выполнены по спирали Архимеда. При одном повороте диска этого патрона кулачки перемещаются на величину радиального расстояния смежных канавок.
Кроме того, форму спирали Архимеда имеют звуковая дорожка на грампластинке и одна из деталей швейных машин - механизм для равномерного наматывания ниток на шпульку.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--