Статья: Непараметрический метод обнаружения гармонического сигналана фоне широкополосного шума

Подставим в (7):

Приведем правую и левую часть неравенства к общему знаменателю:

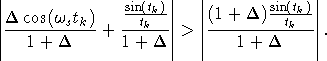
Т. к. , то знаменатель можно отбросить. Раскроем скобки в правой части выражения:

Отсюда:

T. к. , то предыдущее выражение эквивалентно:

Очевидно, что при () . Следовательно . И каким бы ни было , которое нам неизвестно, может быть равен 0 при некоторых моментах корреляции, но не при всех. Т.е. .

Следовательно, алгоритм обнаружения сигнала в шуме можно строить исходя из вычисления канонических дисперсий наблюдаемой выборки.

4. Алгоритм обнаружения

При моделировании будем пользоваться следующей модификацией алгоритма, предложенного в [1].

Шаг 1. На основе выборки { yk} вычисляем ковариационные коэффициенты R(0)=Eyiy'i , R(1)=Eyi+1y'i , R(2)=Eyi+2y'i, R(3)=Eyi+3y'i .

Шаг 2. Строим матрицы:

Шаг 3. Вычисляем разложение:

Шаг 4. Определяем:

Шаг 5. Вычисляем разложение:

-- канонические дисперсии.

Шаг 6. Вычисляем сумму:

S=e1+e2.

Утверждается, что при любом можно устанавливить границу G распознавания гипотез о наличии или отсутствии сигнала так, чтобы Ssh+s>G>Ssh .

Покажем практическую состоятельность этого вывода.

Действительно, зная , можно организовать наблюдения с шагом .