Статья: О движении перпендикулярного луча в эксперименте Майкельсона – Морли
Согласно современной теории относительности никакими экспериментами невозможно обнаружить абсолютное движение Земли. Однако в эксперименте Майкельсона – Морли имеет место движение интерферометра относительно центра Солнца. Так почему же такое относительное движение, вопреки теории относительности, не сопровождается никакими наблюдаемыми явлениями?
Исследование траектории движения перпендикулярного луча
Как известно, основной постулат своей теории относительности Эйнштейн изложил следующим образом:
«...не только в механике, но и в электродинамике никакие свойства явлений не соответствуют понятию абсолютного покоя... для всех координатных систем, для которых справедливы уравнения механики, справедливы те же электродинамические и оптические законы... Это предположение (содержание которого в дальнейшем будет называться «принципом относительности») мы намерены превратить в предпосылку...».
Очевидно, что понятие «абсолютный покой» есть нечто противоположное понятию «абсолютное движение». Тогда постулат Эйнштейна можно сформулировать следующим образом:
«...не только в механике, но и в электродинамике никакие свойства явлений не соответствуют понятию абсолютного движения...».
Во времена Эйнштейна, как и до сегодняшнего дня, под абсолютным движением понимают движение относительно эфира, который Эйнштейн «отменил» своей теорией относительности. Тогда приведенный выше постулат Эйнштейна нужно понимать как невозможность обнаружения движения относительно этого самого эфира. Ну, нельзя, так нельзя. Однако возникает вопрос, а какое именно отношение имеет данный постулат к известному эксперименту Майкельсона – Морли, в котором, как полагают, вопрос о движении Земли относительно эфира был поставлен в наиболее прямой форме. В действительности, однако, это не так: поскольку в данном эксперименте, безусловно, имеет место движение интерферометра относительно центра Солнца, и, следовательно, в наиболее прямой форме был поставлен вопрос именно о том, не сопровождается ли движение интерферометра относительно Солнца, т.е. относительное движение, какими-либо эффектами. Эксперимент подтверждает: не сопровождается. Тогда возникает вопрос, а почему нет, коль скоро появление каких-либо эффектов в результате относительного движения интерферометра не противоречит теории относительности Эйнштейна?
Возникает и еще один вопрос, связанный с движением перпендикулярного луча в этом эксперименте: почему именно этот луч отклоняется в направлении движения интерферометра, в результате чего он всегда попадает в одну и ту же точку на отражателе, независимо от положения интерферометра относительно направления орбитального движения Земли? Попробуем с этим разобраться.
В работе в [1] было показано, что ход лучей в эксперименте Майкельсона – Морли можно рассматривать в двух системах координат, одна из которых связана с Землей (назовем ее движущейся), а другая – с Солнцем (назовем ее неподвижной), относительно которой интерферометр, установленный на Земле, движется с орбитальной скоростью. И хотя наблюдатель в данном эксперименте находится на Земле, сам Майкельсон, как это можно установить из его отчетов, рассматривает ход лучей в интерферометре с точки зрения неподвижного наблюдателя, относительно которого интерферометр движется с орбитальной скоростью Земли. Как же, по мнению Майкельсона движется перпендикулярный луч в его эксперименте? «Луч sa отражается по аb (рис. 1), причем угол bab1 равен углу аберрации α, возвращается по ba1 (aba1 = 2α) θ попадает в фокус зрительной трубы, направление которой не меняется» [2].
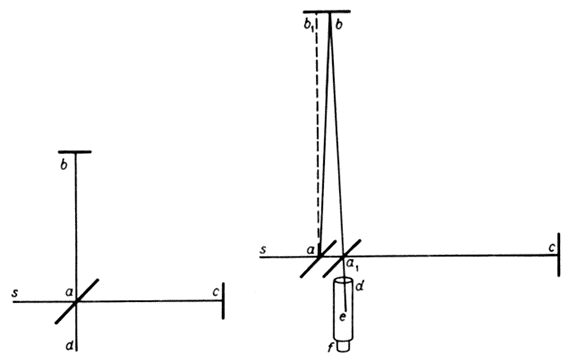
Рис. 1. Траектория движения перпендикулярного луча в эксперименте Майкельсона – Морли
Таким образом, по мнению Майкельсона, перпендикулярный луч отклоняется вслед за смещением интерферометра вследствие аберрации. В действительности, аберрация здесь совершенно не при чем! Как известно, это явление возникает в результате движения приемника света относительно источника. В эксперименте же Майкельсона приемник света и источник неподвижны относительно друг друга. Так почему же, в таком случае, перпендикулярный луч отклоняется вслед за смещением интерферометра, движущегося, напомним, относительно неподвижного наблюдателя?
Итак, предположим для начала, что строго вдоль меридиана Земли со скоростью, скажем, u, движется современный сверхзвуковой самолет. Как выглядит траектория движения этого самолета с точки зрения наблюдателя, неподвижного относительно Солнца? Как и в движущейся системе координат, самолет летит строго вдоль меридиана, но сам меридиан движется перпендикулярно движению самолета с орбитальной скоростью Земли v. В этом случае, согласно законам механики Галилея – Ньютона траектория движения самолета представляет собой гипотенузу прямоугольного треугольника со сторонами u и v, как это изображено на рис. 2:
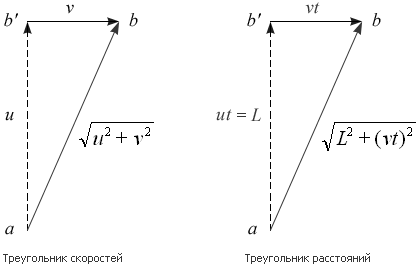
Рис. 2. Треугольник скоростей и треугольник расстояний
За время t, в течение которого в движущейся системе координат самолет пролетит расстояние L между двумя точками a и b, лежащими на меридиане, в неподвижной системе за это же время самолет пролетит путь ab, равный √u2 + v2t. Как следует из треугольника расстояний, в неподвижной системе координат длина пути ab равна √L2 + (vt)2, откуда следует:
√L2 + (vt)2 = √u2 + v2t
L2 + v2t2 = u2t2 + v2t2
L = ut
t = L / u
Таким образом, время, в течение которого самолет пролетит путь L между точками a и b, лежащими на меридиане, оказывается одинаковым и равным t = L / u как в движущейся, так и в неподвижной системах координат.
Предположим, далее, что строго вдоль меридиана проложен линейный ускоритель элементарных частиц, в котором частицы движутся с некоторой скоростью u. Как и в предыдущем случае частицы движутся строго вдоль ускорителя, однако в неподвижной системе координат сам ускоритель смещается с орбитальной скоростью перпендикулярно направлению движению частиц. В этом случае, как было показано выше, траектория движения частиц представляет собой гипотенузу прямоугольного треугольника со сторонами u и v, как это изображено на рис. 1.
За время t, в течение которого в движущейся системе координат движущаяся в ускорителе частица пролетит расстояние L, в неподвижной системе за это же время та же частица пролетит путь ab, равный √u2 + v2t. Как следует из треугольника расстояний, в неподвижной системе координат длина пути ab равна √u2 + v2t, откуда следует:
t = L / u
Таким образом, время, в течение которого частица пролетит путь L в ускорителе, оказывается одинаковым и равным t = L / u как в движущейся, так и в неподвижной системах координат.
Предположим теперь, что строго вдоль меридиана проложен стеклянный стержень длиной L, внутри которого со скоростью u движутся световые импульсы, как это было в эксперименте Шамира и Фокса [3]. Как и в движущейся системе координат в неподвижной системе световые импульсы движутся строго вдоль стеклянного стержня, однако сам стеклянный стержень смещается с орбитальной скоростью перпендикулярно направлению движению световых импульсов. В этом случае, как было показано выше, траектория каждого из световых импульсов представляет собой гипотенузу прямоугольного треугольника со сторонами u и v, как это изображено на рис. 1.
За время t, в течение которого в движущейся системе координат движущийся в стержне импульс пролетит расстояние L, в неподвижной системе за это же время тот же импульс пролетит путь ab, равный √u2 + v2t. Как следует из треугольника расстояний, в неподвижной системе координат длина пути ab равна √L2 + (vt)2, откуда следует:
t = L / u
Таким образом, время, в течение которого импульс света пролетит путь L в стержне, оказывается одинаковым и равным t = L / u как в движущейся, так и в неподвижной системах координат.
Предположим, наконец, что световые лучи движутся в воздухе со скоростью c строго вдоль меридиана, как это было в эксперименте Майкельсона – Морли. Как показали результаты эксперимента, в движущейся системе координат перпендикулярные лучи движутся строго между точками a и b, одна из которых (a) лежит на полупрозрачном зеркале, а другая (b) – на отражателе. Очевидно, и в движущейся системе координат перпендикулярный луч света также должен двигаться между теми же двумя точками: a и b. Таким образом, наблюдается следующая картина: перпендикулярный луч света движется строго вдоль линии между двумя точками a и b, однако сама эта линия смещается относительно неподвижного наблюдателя со скоростью орбитального движения Земли. Тогда, если перпендикулярный луч действительно отклоняется в направлении орбитального движения Земли – а так оно и было на самом деле – то причиной такого отклонения, как и во всех рассмотренных выше случаях, является сложение скорости движения перпендикулярного луча с орбитальной скоростью Земли. В этом случае, согласно законам механики Галилея-Ньютона, траектория движения перпендикулярного луча света представляет собой гипотенузу прямоугольного треугольника со сторонами u и v, как это изображено на рис. 1 (в данном случае u = c). Тогда за время t, в течение которого в движущейся системе координат перпендикулярный луч пройдет расстояние L между точками a и b, в неподвижной системе за это же время тот же импульс пролетит путь ab, равный √c2 + v2t. Как следует из треугольника расстояний, в неподвижной системе координат длина пути ab равна √L2 + (vt)2, откуда следует:
--> ЧИТАТЬ ПОЛНОСТЬЮ <--