Статья: О группах Ассура, фермах Баранова, цепях Грюблера, плоских шарнирных механизмах и об их структурном синтезе
IV
За каждым числовым результатом, приведённым в таблице 1, скрывается своя, порою достаточна содержательная, история. Некоторые из результатов известны уже 130 лет (например, числа 1 и 2 во второй и третьей колонках таблицы 1), другие – 90 лет (например, число 16 в третьей колонке), третьи – 70 лет (например, число 10 во второй колонке), четвёртые – 55 лет (например, числа 1, 1 и 3 в шестой колонке).
В качестве примера остановимся здесь только на синтезе кинематических цепей Грюблера с числом звеньев 10, 12 и 14.
Рядом авторов независимо друг от друга было установлено, что число десятизвенных кинематических цепей равно 230. Первое сообщение о 230 неизоморфных десятизвенных цепях относится к 1967 г. и принадлежит L.S. Woo [1]. В работе [1] приведены схемы всех 230 цепей, каждой из них присвоен свой номер. N.I. Manolescu и I. Tempea получили такой же результат в 1970 году (ссылки на эту и ряд последующих публикаций не включены нами в список литературы). О 230 десятизвенных кинематических цепях сообщают Q. Kiper и D. Schian в 1975 году. T.S. Mruthyunjaya в 1983 году нашёл с помощью разработанной им компьютерной программы 229 десятизвенных цепей, то есть его программа не смогла обнаружить одну десятизвенную цепь (а именно: цепь № 69 из каталога L.S. Woo [1]). Позднее число 230 было подтверждено в ряде публикаций, в том числе в работе [2], выполненной в 1998 году в Германии коллективом авторов (E. Peisach, H. Dresig, J. Schönherr и S. Gerlach).
По сообщению N.I. Manolescu [7], первое упоминание о числе двенадцатизвенных цепей содержалось в докторской диссертации F. Weinhold [3] (1973): им обнаружено 6855 таких цепей. Этот же результат был подтверждён в 1975 г. авторами Q. Kiper и D. Schian. В 1988 г. E.R. Tuttle, S.W. Peterson и J.E. Titus в двух статьях представили алгоритм, основанный на теории групп, с помощью которого они нашли 6856 двенадцатизвенных кинематических цепей, т. е. на одну больше по сравнению с ранее полученным результатом. Несколько иной результат, а именно 6862 цепи, был получен авторами W.-M. Hwang и Y.-W. Hwang в 1992 году. J. Srinath и S. Krishnamurty в 1995 году нашли 6856 кинематических цепей с 12 звеньями, что совпадает с одним из полученных ранее результатов. Разница в полученных разными авторами результатах (6855, 6856 и 6862), хотя и небольшая, потребовала ещё ряда независимых экспертиз. Программа, представленная в уже упомянутой выше работе [2], выполненной в 1998 году коллективом авторов, синтезировала 6856 неизоморфных двенадцатизвенных кинематических цепей. Точно такой же результат был получен в 2005 году авторами E.A. Butcher и C. Hartman [4]. Таким образом, есть основания полагать, что найденное значение 6856 является правильным.
Что касается синтеза 14-звенных цепей Грюблера, то на сегодняшний день имеются только две посвящённые им публикации. Впервые их общее число, оказавшееся равным 318162, было получено в 1998 году и представлено в упомянутой выше работе [2]. Точно такое же значение числа 14-звенных цепей было найдено в 2005 году в статье [4]. Авторы этой статьи E.A. Butcher и C. Hartman утверждают, что они первыми решили данную задачу. Скорее всего, они получили свой результат независимо (видимо, им было не известно, что задача была решена за семь лет до выхода их статьи). Удивительное совпадение полного числа 14-звенных кинематических цепей, найденное двумя независимыми группами исследователей при помощи разных алгоритмов и программ, с большой степенью вероятности свидетельствует о правильности результата.
V
Изложенные выше соображения позволяют заключить, что в структурном синтезе четырёх рассматриваемых объектов есть зона, в пределах которой задачи синтеза решены окончательно, и нет особого смысла вновь и вновь заниматься их решением, поскольку не приходится ожидать, что может быть получен какой-либо иной результат, кроме уже известного. Если же при решении задачи, относящейся к указанной зоне, получается результат, отличный от общеизвестного, то, как правило, он является ошибочным.
Для иллюстрации сказанного обратимся к двум недавним публикациям [5] и [6]. В этих статьях утверждается, что число семизвенных ферм Баранова не 3, а 5; число восьмизвенных цепей Грюблера не 16, а 20; число шестизвенных шарнирных механизмов не 9, а 7; число восьмизвенных шарнирных механизмов не 153, а 158; число восьмизвенных групп Ассура не 173, а 160 (по данным на с. 40 статьи [5]) или 167 (по данным на с. 31 статьи [5]), число девятизвенных ферм Баранова не 28, а 26 (если судить по рис. 5 на с. 33-34 статьи [5]).
Все перечисленные утверждения являются ошибочными. Кроме того, в статьях [5] и [6] имеется немало и других неточностей и ошибочных утверждений и выводов (о них будет кратко сказано ниже).
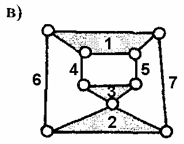
О семизвенных фермах Баранова и их числе. В 1952 году Г.Г. Баранов получил три таких фермы [7]. В последующие годы этот результат воспринимался как очевидный факт. Однако авторы статьи [5] считают, что число семизвенных ферм равно пяти; они приводят на рис. 3 три фермы Баранова (№1, №2 и №3), а на рис. 4 - две дополнительные фермы. Ниже на рис. 2 показаны фермы №1 и №3 Баранова и две дополнительные фермы, полученные авторами статьи [5].
|
Фермы Баранова (по рис. 3 из статьи [5]) |
"Новые" фермы (по рис. 4 из статьи [5]) |
Матрица структурной схемы |
|
|
|
|
|
|
|
|
|
Рис. 2 | ||
Из рис. 2 видно, что первая дополнительная ферма (см. рис. 4(а) в [5]) идентична по своей структуре ферме №1 Баранова, а вторая дополнительная ферма (см. рис. 4(b) в [5]) идентична ферме №3 Баранова. В том же самом можно убедиться, если составить структурную матрицу S для каждой из четырёх указанных структур (см. на рис. 2 справа). Элемент ![]() матрицы S равен 1, если звено номер i связано шарниром со звеном номер k, и равен 0 в противном случае (i, k = 1, 2, …, n; n = 7).
матрицы S равен 1, если звено номер i связано шарниром со звеном номер k, и равен 0 в противном случае (i, k = 1, 2, …, n; n = 7).
Таким образом, нет оснований для пересмотра общеизвестного факта о том, что число семизвенных ферм Баранова равно трём.
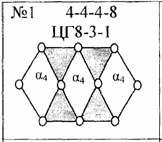
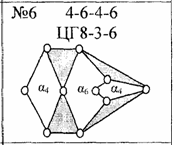
О восьмизвенных цепях Грюблера и их числе. Как известно, число восьмизвенных цепей Грюблера равно 16. Схемы всех этих цепей приводятся во многих учебниках по теории механизмов, изданных в Германии, а также в ряде англоязычных изданий. Однако авторы статьи [5] утверждают, что в статье [6] "убедительно показано, что восьмизвенных цепей Грюблера в действительности не 16, а 20" (см. с. 31). А в статье [6] сказано, что в ней "впервые приводятся новые виды цепей Грюблера, которые ранее известны не были" (см. с. 94). В таблице 2, озаглавленной "Полный состав восьмизвенных цепей Грюблера" (см. с. 91-92 статьи [6]) приведены рисунки всех 20 полученных авторами восьмизвенных цепей, и им присвоены номера от №1 до №20.
Анализ этой таблицы позволил установить, что среди 20 изображённых там цепей Грюблера только 16 цепей являются неизоморфными, а 4 пары цепей встречаются в таблице дважды. Так, цепи №1 и №6, №11 и №14, №12 и №17, №19 и №20 являются попарно одинаковыми по своей структуре. Четыре указанных пары кинематических цепей показаны здесь на рис. 3 (они получены сканированием соответствующих изображений из статьи [6]).
|
|
|
|
К-во Просмотров: 343
Бесплатно скачать Статья: О группах Ассура, фермах Баранова, цепях Грюблера, плоских шарнирных механизмах и об их структурном синтезе
|