Статья: О методике решения задач на относительность движения при изучении основ кинематики в 9 классе об

V2 = V - V1

-V1 = V2 – V

V1 = V – V2

V1 = 80 км/ч - 60 км/ч = 20 км/ч

Ответ: скорость второго относительно первого поезда равна 20 км/ч.

Задача №2

Скорость течения реки V= 1,5 м/с. Каков модуль скорости V1 катера относительно воды, если катер движется перпендикулярно к берегу со скоростью V2 = 2 м/с относительно него.

1. Дано:

V= 1,5 м/с За НСО примем берег реки,

V2 = 2 м/с за ПСО – реку (скорость течения реки V),

V - ? движущееся тело – катер.

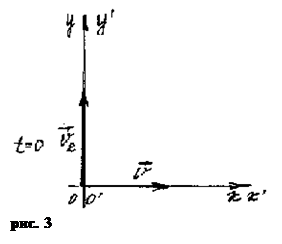
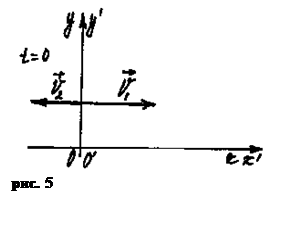
2. Закон сложения скоростей V2 = V + V1. Скорость катера относительно НСО (берега реки) равна геометрической сумме скорости катера относительно ПСО (течения реки) и скорости течения реки.

3. Свяжем НСО с системой координат XY, а ПСО с системой координат X`Y`. Ось OX направим вдоль берега, а ось OY поперек реки (O`X` и O`Y` соответственно).

4.

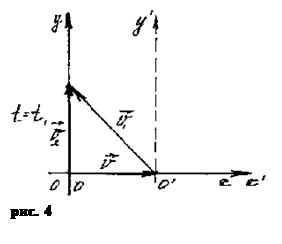
5. Сравним закон сложения скоростей и графика. Для простоты решения найдем геометрическую сумму векторов скорости.

6. Так как полученный треугольник прямоугольный, то

Ответ: модуль скорости катера относительно реки 2,5 м/с.

Задача № 3

Два поезда движутся навстречу друг другу со скоростями 72 и 54 км/ч. Пассажир, находящийся в первом поезде, замечает, что второй поезд проходит мимо него в течение 14 с. Какова длина второго поезда ?

1. Дано:

V1 =72 км/ч =20 м/с Так как движение поездов можно считать равномерным,

V2 = 54 км/ч = 15 м/с то длину второго поезда можно найти по формуле

l - ? l = V21× t, где V21 – скорость второго поезда относительно первого поезда. Значит, для определения l необходимо найти V21.

Примем за НСО Землю, а за ПСО – первый поезд, движущееся тело – второй поезд. V2 скорость второго поезда относительно НСО. Скорость ПСО - V1.

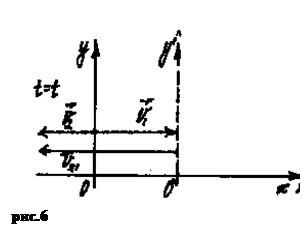
2. Закон сложения скоростей V2 = V2 1 + V1. Скорость второго поезда относительно НСО равна геометрической сумме скорости второго поезда относительно ПСО (первого поезда) и скорости ПСО (первого поезда).

3. 4.