Статья: О методике решения задач на относительность движения при изучении основ кинематики в 9 классе об

Одним из сложных и недостаточно разработанных вопросов методики физики является методика решения задач на относительность движения. Анализ специальной литературы и имеющийся практический опыт убеждают в том, что учащиеся школы и студенты не умеют решать задачи на относительность движения. В методических пособиях предлагается преимущественно логические приемы решения, иллюстрируемые иногда рисунками.

Мы предлагаем способ решения задач на относительность движения, который позволяет конкретизировать представления учащихся и студентов о законе сложения скоростей и перемещений, о понятии неподвижной системы отсчета (НСО) и подвижной системы отсчета (ПСО). Учит определять скорости, перемещения тел относительно различных систем отсчета (СО) и другие величины, убеждает в относительности скорости и перемещения тел.

Сущность предлагаемого способа решения задач сводится к следующему алгоритму:

Анализ условия задачи, выделение движущихся тел. Краткая запись условия задачи. Определение неподвижной и подвижной системы отсчета (НСО и ПСО), движущегося тела.

Записать закон сложения скоростей или перемещений в векторной форме.

Изобразить графически параметры заданных движений, при этом выбрать начальный момент времени и совместить начало НСО и ПСО.

Отобразить на графике, который строится под первоначальным, изменение величин, описанных в задаче со временем.

Сравнение закона сложения скоростей (перемещений) и графика.

Записать закон сложения скоростей (перемещений) в проекциях на оси координат, объединив их в систему (или найти геометрическую сумму путем сложения векторов).

Решить полученную систему уравнений. Подставить в решение общего вида значения величин и произвести вычисления.

На примерах решения типовых задач на относительность движения покажем применение данного способа решения.

Задача № 1.

Два поезда движутся равномерно друг за другом. Скорость первого 80 км/ч, а второго 60 км/ч. Какова скорость второго поезда относительно первого ?

1. Первый и второй поезда движутся относительно Земли с некоторыми скоростями. Скорость первого поезда V, скорость второго V2 (жирным шрифтом обозначены векторные величины).

Дано: Решение:

V = 80 км/ч За НСО примем Землю, за ПСО – первый поезд.

V2 = 60 км/ч Скорость ПСО относительно НСО – V.

V1 - ? Движущимся телом является второй поезд.

Скорость движущегося тела относительно НСО – V2.

Неизвестная скорость второго поезда относительно первого (ПСО) – V1.

2. Закон сложения скоростей V2 = V + V1. Скорость второго поезда относительно НСО равна геометрической сумме скорости второго поезда относительно ПСО и скорости ПСО относительно НСО.

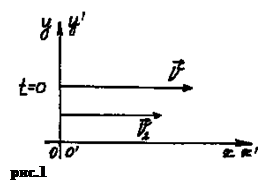
3. Систему координат XY свяжем с Землей (НСО).

Систему координат X¢ Y¢ параллельную XY свяжем с первым поездом (ПСО)

В начальный момент времени (t = 0) совместим НСО и ПСО.

4. Через t = 1 час положение ПСО (первого поезда) изменится на расстояние, равное 80 км, а второго поезда, относительно НСО окажется на расстоянии 60 км.

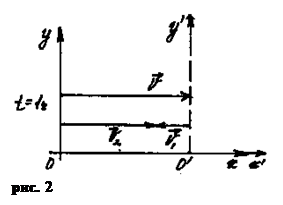
5. Соотнесем график и формулу закона сложения скоростей V2 = V + V1. Убеждаемся в том, что обе формы отражения закона совпадают.

6. Для вычисления скорости второго поезда относительно первого найдем проекции и запишем:

V2x = Vx + V1x

--> ЧИТАТЬ ПОЛНОСТЬЮ <--