Статья: PageRank: анализ потоков

В первой части статьи было установлено, что итерационные методы не имеет смысла применять для расчетов PageRank, учитывающих окружение сайта и "входящий" PR. Поэтому мы будем рассчитывать PageRank страниц не в численном виде, а виде функций от входящего PR. Это позволит выделить ту компоненту PageRank, которая увеличивается по мере раскрутки, и отделить "остатки" в виде констант, величина которых порядка единицы.

Повторение: функциональный метод расчета PageRank

Задача: рассчитать стабильные значения PageRank, не применяя итерационных методов. Рассмотрим уравнение (1) внимательнее - в нем нет никаких особенностей, которые требуют применения итераций. Наоборот, PR каждой страницы определяется как функция PR других страниц. Предположим, что мы достигли стационарного состояния, и PageRank страниц не меняется. Остается только записать уравнения для PR каждой из страниц и решить систему.

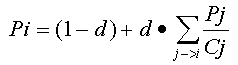{1}

Итак, будем рассчитывать PageRank страниц сайта как функцию от внешнего, "входящего" PageRank. Для этого нужны: уравнение (1) и представление об эквивалентности страниц одного типа. Пример-

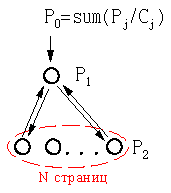
На сайте, который приведен ниже, 3 нижних страницы эквивалентны между собой во всех смыслах. Соответственно, все они будут иметь одинаковый PageRank (P2). Головная страница отличается от них и имеет PR=P1.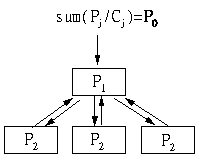

Запишем уравнения для страниц вида 1 и вида 2:

P1=0.15+0.85*(P0+3P2) - на страницу вида 1 ссылаются 3 страницы вида 2, на каждой из которых есть одна ссылка.

P2=0.15+0.85*(P1/3) - на страницу вида 2 ссылается страница вида 1, на которой есть 3 ссылки.

Решая эту систему, получаем-

P1=0.15*(1+3*0.85)/(1-0.85^2)+0.85/(1-0.85^2)*P0=1.92+3.06*P0 P2=0.69+0.87*P0

Этим методом хотя и сложнее пользоваться, но он обладает одним хорошим качеством, которого нет у итерационных методов - общностью.

Различные случаи: два типа страниц

Итак, начнем рассмотрение самого простого случая - сайт состоит из одной головной страницы и некоторого количества подчиненных страниц. Ссылки извне направлены на головную страницу.

Случай 1: "метла"

С головной страницы (PageRank=P1) есть ссылки на N эквивалентных подчиненных страниц (PageRank=P2). Подчиненные страницы не связаны между собой, на каждой из них есть одна ссылка на головную страницу.

Система уравнений: (N>=1) P1=0.15+0.85*(P0+N*P2) - на страницу вида 1 ссылаются N страниц вида 2, на каждой из которых 1 ссылка P2=0.15+0.85*(P1/N) - на страницу вида 2 ссылается одна страница вида 1, на ней N ссылок

Решая систему, находим зависимости P1, 2 от P0, N.

Решение системы: P1=0.15/(1-0.85^2)+0.85*0.15/(1-0.85^2)*N+0.85^2/(1-0.85^2)*P0 =>

P1=0.541+0.459*N+3.063*P0 P2=0.541+0.459/N+2.604*P0/N

Итак, мы видим, что:

PageRank главной страницы (P1) увеличился не на P0, но на 3P0. Т.е, мы получаем реальный выигрыш за счет взаимного влияния страниц

P2 обратно пропорционален числу страниц. Очевидный вывод.

P1 прямо пропорционален числу страниц. Следовательно, увеличивая количество страниц на сайте, можно сконцентрировать большой PageRank на главной странице. При этом P2 по мере увеличения количества страниц стремится к 0.541, а не к 1; и отдает часть PageRank главной странице

Средний PR

Рассчитаем суммарное значение PageRank по нашему сайту-

--> ЧИТАТЬ ПОЛНОСТЬЮ <--