Статья: PageRank: начала анализа

4

1

0

0

0

Здесь страница 1 ссылается на 2, 3, 4; страница 2 - на 3 и 4; страница 3 на 4, а 4 на 1. Представленная матрица содержит значения Mij=1/Cj->i, т.е. значение в каждой ячейке разделено на общее количество ссылок Cj на странице j.

Недостатки численных и итерационных методов

Фактически, оба приведенные выше метода являются разными формулировками итерационного метода расчета значений PageRank. Они требуют работы с конкретными численными значениями PageRank. Методы использованы для расчетов в работах [3,4].

Однако, рассмотрим реальную ситуацию. Для того, чтобы воплотить в жизнь свои знания о распределении PageRank, необходима индексация ваших страниц. В случае Google, ваш сайт не будет проиндексирован (либо придется ждать индексации очень долго) до достижения некоего порогового значения PageRank. В любом случае, на ваш сайт должны существовать ссылки, хотя бы одна. Это значит, что ваш сайт не оторван от "внешнего мира", и существует ненулевой "входящий PageRank", направленнный извне на ваш сайт.

Из этого рассуждения следует, что:

Расчеты PR "в отрыве" от окружения сайта неточны для каждой страницы вашего сайта - они проделаны для нулевого входящего PageRank

Правило нормировки не работает в пределах вашего сайта (но работает в пределах глобального набора проиндексированных страниц, т.е. в рамках Интернет по версии Google)

Никакой численный расчет не может применяться в динамике - ведь входящий PageRank изменяется по мере раскрутки сайта (если вы дочитали до этого места, вероятно, раскруткой своего сайта будете заниматься так же упорно). Соответственно, меняется во времени PR каждой страницы.

Стоит помнить о том, что по своей сути PageRank - это поток (поток теоретической посещаемости). Соответственно, расматривая свой сайт как "маленькую вселенную", вы не учитываете потоки извне. Если применить аналогию, такой сайт похож на высохшее озеро, на дне которого осталось несколько луж, и вы рассчитываете, в какой из них будет больше воды.

Посмотрим, что происходит при увеличении входящего PageRank.

Вот простейший сайт из четырех страниц, ссылок извне нет-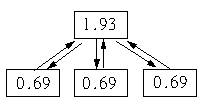

А здесь входящий PageRank равен единице-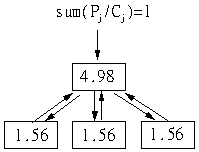

Но нам скоро станет лень рассчитывать PageRank при каждом "воображаемом" изменении внешнего PageRank (P0). Поэтому рассмотрим общий случай и выразим PR страниц как функции от P0-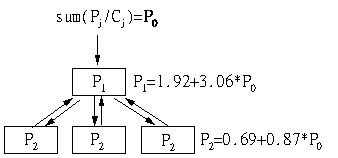

В дальнейшем будем рассчитывать PageRank страниц как функции от входящего PR. Это позволит выделить ту компоненту PageRank, которая увеличивается по мере раскрутки, и отделить "остатки" в виде констант, величина которых порядка единицы. А солипсистскими методами расчета пользоваться на будем - мы ведь не одни в Интернете...

Функциональный метод расчета PageRank

Задача: рассчитать стабильные значения PageRank, не применяя итерационных методов. Рассмотрим уравнение (1) внимательнее - в нем нет никаких особенностей, которые требуют применения итераций. Наоборот, PR каждой страницы определяется как функция PR других страниц. Предположим, что мы достигли стационарного состояния, и PageRank страниц не меняется. Остается только записать уравнения для PR каждой из страниц и решить систему.

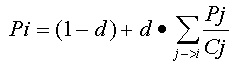{1}

Итак, будем рассчитывать PageRank страниц сайта как функцию от внешнего, "входящего" PageRank. Для этого нужны: уравнение (1) и представление об эквивалентности страниц одного типа. Пример-

На сайте, который приведен ниже, 3 нижних страницы эквивалентны между собой во всех смыслах. Соответственно, все они будут иметь одинаковый PageRank (P2). Головная страница отличается от них и имеет PR=P1.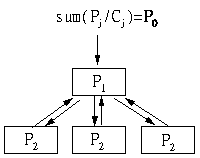

Запишем уравнения для страниц вида 1 и вида 2:

P1=0.15+0.85*(P0+3P2) - на страницу вида 1 ссылаются 3 страницы вида 2, на каждой из которых есть одна ссылка.

P2=0.15+0.85*(P1/3) - на страницу вида 2 ссылается страница вида 1, на которой есть 3 ссылки.

Решая эту систему, получаем-

P1=0.15*(1+3*0.85)/(1-0.85^2)+0.85/(1-0.85^2)*P0=1.92+3.06*P0 P2=0.69+0.87*P0

Этим методом хотя и сложнее пользоваться, но он обладает одним хорошим качеством, которого нет у итерационных методов - общностью.