Статья: Применение объектно-ориентированного программирования в параметрическом анализе структур Тьюринга

3. Бифуркационный анализ.

Нахождение стационарных точек ( далее - ст.с) заключается в поиске решений системы уравнений:

(8)

Вторым шагом исследования системы (1) является определение характера особых точек и построение параметрических кривых.

При изучении поведения динамической модели (1) обычно недостаточно знать ее характеристики только при одном конкретном значении того или иного параметра, важно иметь представление о характере поведения модели в зависимости от значений параметров, изменяющихся в выбранном диапазоне. В общем случае эта задача связана с решением нелинейных систем с параметрами. В результате чего получаем зависимости:

(9)

где - это параметры из (2), (3).

Последним этапом параметрического анализа является построение бифуркационных кривых: кривой кратности стационарных состояний LΔ: Δ=0 и кривой нейтральности Lσ,: σ=0.

Опишем процедуру построения этих кривых.

Пусть система (1) имеет однородное по пространству стационарное состояние (,). Исследуем его устойчивость, принимая во внимание, что неподвижными (особыми или стационарными) называются точки, положение которых на фазовом портрете с течением времени не изменяется.

Для этого запишем линеаризованную относительно отклонений систему:

,

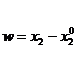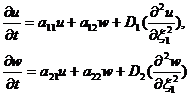(10)

Сформируем матрицу Якоби с элементами

(11)

где

(12)

Будем искать решение в виде:

, (13)

при котором характеристическое уравнение примет вид:

(14)

где

(15)

(16)

Значение x определено ст.с. Устойчивость ст.с. определяется собственными числами матрицы Якоби. Для исследования устойчивости достаточно исследовать знак σ и Δ.

Выделим из два параметра p1 и р2 и построим линии LΔ и Lσ в плоскости этих параметров. Граница области множественности LΔ определяется, как решение системы уравнений:

H(x,p1,p2) = 0

Δ(x,p1,p2)=0