Статья: Применение объектно-ориентированного программирования в параметрическом анализе структур Тьюринга

Процедура предназначена для получения параметрических зависимостей кривой кратности (LΔ) относительно двух параметров.

Таблица №1. Основные методы класса TModel

Остальные методы и параметры класса TModel предназначены для задания начальных условий и взаимодействия с внешними классами.

2.2 Численные методы

Для каждого шага исследования необходимо применять свой метод расчетов, однако, ООП позволяет создать ряд основных вычислительных механизмов, с помощью которых можно численно рассчитать все необходимые уравнения. Стоит отметить, что каждый из рассматриваемых методов представляет собой набор численных алгоритмов не привязанных к конкретной функции. Таким образом любой метод можно представить в виде метода некоторого общего класса. Входными параметрами данного метода будут являться функции, выше они описаны в виде класса TFtp, и переменные которые следует получить. Рассмотрим численные методы по каждой стадии параметрического анализа.

2.2.1 Нахождение стационарных точек системы

В этом случае достаточно применение метода последовательных разбиений на отрезки. Условие (4) позволяет взять достаточно малый шаг h от которого и зависит точность решения.

2.2.2 Исследование устойчивости стационарных точек

Задачу по исследованию стационарных точек необходимо разбить на три стадии. На первой стадии выясняется условие вхождения исследуемого параметра в систему. Для большей наглядности рассмотрим данный этап на примере построения параметра из (7). Благодаря тому, что параметр входит лишь в одно уравнение системы (7), мы можем получить значения x1 x2 из второго уравнения методом дихотомии, с высокой степенью точности. Подставляя, таким образом, x1 x2 в функцию F и повторно применяя метод дихотомии, но уже для мы получим искомую зависимость.

Необходимо отметить, что условия вхождения параметра только в одно уравнение справедливо и для других систем поскольку вытекает из методики построения данных уравнений. В случае применения указанного алгоритма для систем уравнений, полученных из иной предметной области или же при рассмотрении структур Тьюринга для трех переменных, где такое условие уже не действует, следует применять иные вычислительные алгоритмы, например, рассмотренный ранее метод последовательного разбиения на отрезки.

2.2.3 Бифуркационный анализ

Для бифуркационного анализа рассмотрим методику построения кривой нейтральности, используя систему уравнений (7). Для примера возьмем зависимость:

. (17)

В этом случае уравнение (17) имеет нелинейный вид относительно своих переменных и единственный метод нахождения корней – это метод последовательного разбиения на отрезки по параметру . В результате, чего мы получаем искомую кривую.

2.3 Интерфейс

Интерфейс программного обеспечения представляет собой набор классов с методами предназначенными для отображения информации полученной на предыдущих этапах. Данный блок программы не привязан к вычислительным процедурам и в общем случае может применяться для любых иных целей, где есть надобность в последовательном отражении информации схожей с той, что получается при расчетах в рассматриваемой модели. Выделим три основных компонента интерфейса программы, каждый из которых являет собой некий класс.

I. Класс TGraph - предназначен для отображения графиков получаемых при построении параметрических зависимостей (Рис №2), а так же фазовых портретов при решении системы дифур и графиков динамики изменения концентрации вещества при численном счете (1). Данный класс во внешнем интерфейсе имеет лишь один метод AddXY(X,Y : Real), предназначенный для внесения очередной точки-параметра на плоскость. Масштабирование, фокусировку, выделение области и смещение класс TGraph осуществляет самостоятельно.

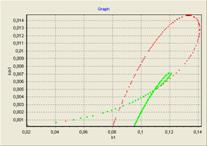
Рис. №2. Пример работы класса TGraph

II. Класс TPlant – предназначен для отображения степени концентрации вещества на пластине при решении (1) в двумерном случае. Данный класс, как и предыдущий содержит в себе только один метод предназначенный для внесения точки на плоскость и применяется уже не при исследовании, а расчете модели. На Рис №3 показан пример такого отображения.

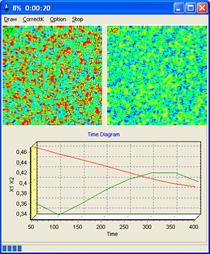
Рис. №3. Пример работы класса TPlant

III. Класс TCube – предназначен для отображения степени концентрации вещества в объеме при решении (1) в трехмерном случае. Интерфейс данного класса содержит значительное количество методов и параметров предназначенных для вращения, сечения, масштабирования, смещения, а так же ряд специфических функций необходимых исследователю. Метод с помощью которого добавляется точка в куб имеет лишь одно отличие от ранее рассмотренных, а именно дополнительную координату.

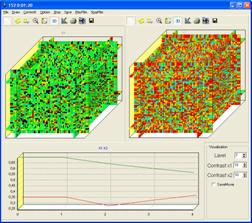
Рис. №4. Пример работы класса TCube

3. Сравнительный анализ предложенного метода и альтернативных решений

Альтернативных методов решения поставленной задачи может быть два, а именно: аналитические решения и решения с помощью прикладных продуктов, например Matlab.

Преимущества перед аналитическим методом вполне очевидны, поскольку перекладывают всю работу по поиску решений на компьютер, тем самым, избавляя исследователя от кропотливой работы выведения всех необходимых зависимостей.

К примеру, функция кривой нейтральности для предложенного примера (6), выглядит следующим образом: