Статья: Радиационные пояса

В настоящем разделе мы кратко рассмотрим особенности движения заряженных частиц в магнитном и электрическом полях в магнитосфере Земли. С более подробным изложением этих вопросов можно ознакомиться в (Альвен, Фельтхаммер, 1967; Лайонс, Вильямс, 1987; Chen, 1970).

1.1 Движение частиц в геомагнитном поле

Значительная часть частиц радиационных поясов находится в магнитном поле, основным источником которого являются токи внутри Земли. Они создают поле близкое к дипольному. Краткие характеристики этого поля на 2005 г.: ось диполя наклонена к оси Земли на 10.26° и на поверхности Земли имеет координаты 79.74°N и 71.8°W; центр диполя сдвинут относительно центра Земли на ~ 500 км. Магнитное поле диполя в плоскости экватора геомагнитного диполя меняется по закону:

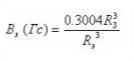(3.2.1)

где Rэ – расстояние от центра диполя, Rз – радиус Земли. Силовая линии дипольного поля описывается формулой

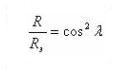(3.2.2)

где λ – геомагнитная широта. Дипольное поле меняется вдоль силовой линии как

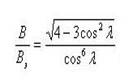(3.2.3)

При анализе распределения частиц радиационных поясов в магнитосфере Земли необходимо исходить из структуры и физических свойств магнитосферы. Во-первых, необходимо учитывать недипольность геомагнитного поля на больших расстояниях, вызванную давлением солнечного ветра. Во-вторых, многие явления в магнитосфере могут быть объяснены при предположении существования в магнитосфере Земли квазиоднородного электрического поля величиной 10-6 – 10-5 В/см, направленного с утра на вечер.

Движение частиц c Е < 1 ГэВ в дипольном поле можно представить как суперпозицию трех независимых движений: ларморовского вращения частицы в плоскости перпендикулярной магнитному полю; колебания мгновенного центра вращения (ведущего центра) вдоль силовых линий и дрейфа ведущего центра вокруг Земли.

Ларморовское вращение совершается с периодом τ1:

(3.2.4)

где Е - кинетическая энергия частицы в МэВ, Е0 - энергия покоя частицы в МэВ (для электрона Е0= 0.51 МэВ, для протона Е0= 938 МэВ) и В – магнитное поле в Гс.

Ларморовская частота 1/τ1 электронов вблизи Земли ~1 MГц, протонов – ~1 кГц, при удалении от Земли частота уменьшается как 1/Rз. Ларморовский радиус вращения частицы

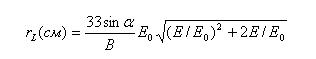
(3.2.5)

где p ⊥ - поперечный импульс частицы, с – скорость света и α - угол между векторами скорости частицы и локального магнитного поля (питч-угол). Здесь В выражено в Гс, p⊥ с - в эВ, Е и Е0 в МэВ.

Ларморовский радиус электронов радиационных поясов в геомагнитном поле не превосходит нескольких километров, а для протонов его величина может достигать нескольких сотен километров.

В процессе движения частицы вдоль силовой линии выполняется соотношение sin2<α /B=const. Отсюда, зная питч-угол α на экваторе, можно определить напряженность поля в точке отражения:

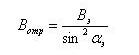(3.2.6)

Период колебания частицы между точками отражения

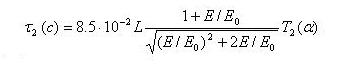(3.2.7

где Т2 (α)= 1,3-0,563 sin αэ.

Дрейф вокруг Земли по долготе для частиц с разными знаками заряда происходит в противоположных направлениях (электроны движутся на восток, протоны – на запад). Период дрейфа вокруг Земли

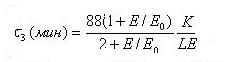(3.2.8)

где K= 1,25-0,25 cos 2λm, λm – геомагнитная широта точки отражения, Е – в МэВ.

Для нерелятивистских частиц τ3= 44/(EL).

Рассмотренным периодическим движениям соответствуют некоторые величины, сохраняющиеся (в среднем) при движении частицы, если за время, характерное для данного типа движения: (τ1,τ2,τ3), изменением магнитного поля можно пренебречь:

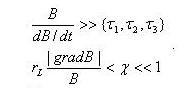(3.2.9)

Эти величины называются адиабатическими инвариантами движения частиц.

Первым адиабатическим инвариантом является магнитный момент частицы

--> ЧИТАТЬ ПОЛНОСТЬЮ <--