Статья: Решение иррациональных неравенств

Нашим читателям наверняка знакомы такие обороты речи как «мыслить штампами», «выполнять работу по сложившемуся стереотипу». К сожалению, многие ребята, при решении задач действуют по стереотипу. Если же условия задачи не подходят под известный алгоритм, то они нередко вольно или невольно изменяют (или дополняют) условия задачи так, чтобы она подходила под этот алгоритм.

При проверке решений задач на олимпиадах и вступительных экзаменах, автору нередко приходится сталкиваться с тем, что ученик произвольный треугольник заменяет правильным или равнобедренным. Часто, рассматривая четырехугольник с перпендикулярными диагоналями, учащиеся объявляют его ромбом (а ведь для этого нужно, чтобы диагонали в точке пересечения делились пополам). Список таких «превращений» можно продолжать и продолжать.

Кроме того, очень ценным качеством умного человека является умение нестандартно мыслить, решать нестандартные задачи.

Для вас «нестандартные» – это такие задачи, способ решения которых не изучался ранее. Само слово «нестандартный» не должно вас пугать. Очень часто нестандартное решение проще, понятнее и красивее (но отнюдь не сложнее), чем стандартное, шаблонное решение.

Дадим несколько практических советов, которые помогут вам избежать ошибок, связанных со стереотипами и позволят находить решения нестандартных задач на уроках геометрии.

Итак, во-первых, внимательно вдумайтесь в описание геометрической фигуры, о которой идет речь в условиях задачи. Проанализируйте, достаточно ли «хороших» признаков для того, чтобы рассматриваемая фигура (например, треугольник) была «хорошей» (правильной).

Если окажется, что данные в условии признаки не совпадают с известными условиями «правильности» фигуры, то, во-вторых, попытайтесь вывести (доказать) недостающие признаки.

Если же и это не поможет, тогда попробуйте (в-третьих) придумать пример «неправильной» фигуры, обладающей описанными в задаче свойствами (это называется контрпример).

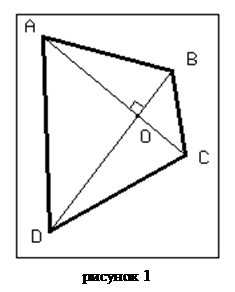????????, ????? ?????????, ??? ?????????????????? ??????????, ?????? ?? ???, ??? ????? ?????, ????????? ??? ????????????????, ?????????????? ???????. ??? ???? ????????????, ????? ????? ??????????? ???? ???????? ?? ?????? ??????? ?? ???? ?? ???. ????? ????????? (??. ???.1), ??? ????? ???????? ????? ????????? ????????????????, ?? ??????????? ??????.

Теперь о том, как находить нестандартные решения.

Для этого бывает полезно вспомнить всевозможные свойства той или иной фигуры, не совпадающие с определением этой фигуры.

Например, мы знаем, что центр описанной окружности треугольника это точка пересечения его серединных перпендикуляров. Однако есть и еще одна ценная характеристика этой точки. Дело в том, что центр описанной окружности удален от всех вершин на одинаковое расстояние.

Кроме того, нередко удается найти решение новой задачи, применяя общие математические принципы и подходы.

Далее вашему вниманию предлагается несколько задач (некоторые с указаниями и советами), которые помогут вам (я надеюсь) побороть некоторые штампы и стереотипы. Кроме того, решение некоторых из них потребует нестандартных подходов.

Задачи для самостоятельного решения

Уважаемые ребята, ниже приводятся задания для самостоятельного решения, которые следует выполнить, оформить отдельно от заданий по другим предметам и выслать в адрес Хабаровской краевой заочной физико-математической школы.

М10.9.1. Определите, какие признаки достаточны для указанной фигуры, а какие нет. Придумайте контрпримеры. Если признаков недостаточно, дополните их.

Если у многоугольника все стороны равны, то он – правильный.

Если у многоугольника все углы равны, то он – правильный.

Если у треугольника все высоты равны – он правильный.

Если у треугольника высоты и медианы, проведенные из одной вершины, равны, то он правильный.

Если четырехугольник вписан и описан вокруг окружности, то он квадрат.

Если медианы треугольника равны, то он правильный.

Если все высоты четырехугольника равны, то он: а) квадрат; б) ромб; в) параллелограмм.

Замечание: высота в данном случае есть перпендикуляр, опущенный из вершины на противоположную сторону.

Если медианы и высоты, проведенные из двух вершин треугольника соответственно равны, то он правильный.

Если биссектрисы поделили треугольник на 6 равных по площади треугольников, то он правильный.

Следующие задачи – на нестандартные ситуации

на уроках.

М10.9.2. У школьника Пети нет циркуля, зато есть бумажный кружок. Пете нужно построить окружность (ну хоть какую-нибудь) и найти ее центр.

Помогите Пете.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--