Статья: Решение текстовых задач

Так как по условию в пункте D поезда встретились, они затратили на путь до встречи одинаковое время, поэтому получаем первое уравнение

.

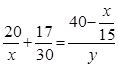С другой стороны, выразим время движения поездов после встречи в пункте D.

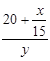Так как , то – время движения поезда из В после встречи.

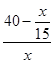Так как , то – время движения поезда из А после встречи.

По условию .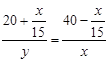

Таким образом, мы составили систему двух уравнений с двумя переменными.

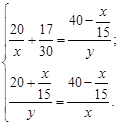
Решим систему, для чего из первого уравнения выразим у и подставим это выражение вместо у во второе уравнение.

;

;

.

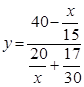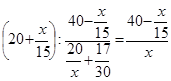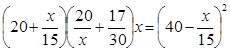Решим полученное уравнение

;

;

;

х1=60; х2=–600.

Так как х – скорость, то х2 не подходит по смыслу задачи. Подставим полученное значение х в выражение для у

.

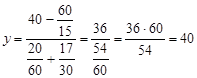Ответ: vA=60 км/ч, vB=40 км/ч.

Задачи на совместную работу

Содержание задач этого типа сводится обычно к следующему: некоторую работу, объем которой не указывается и не является искомым, выполняют несколько человек или механизмов, работающих равномерно, то есть с постоянной для каждого из них производительностью. В таких задачах объем всей работы, которая должна быть выполнена, принимается за 1; время t, требующееся для выполнения всей работы, и р – производительность труда, то есть объем работы, сделанной за единицу времени, связаны соотношением

.

Рассмотрим стандартную схему решения задач этого типа.

Пусть х – время выполнения некоторой работы первым рабочим,

у – время выполнения этой же работы вторым рабочим.

Тогда – производительность труда первого рабочего,

– производительность труда второго рабочего.

– совместная производительность труда.