Статья: Структура рекурсивных m-степеней в полях

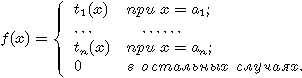
Непосредственно из определения следует, что для любого конечного Y.

Следствие 7. Справедливы следующие утверждения:

1) если X конечное рекурсивное множество и , то любое конечное рекурсивное Y сводится к X;

2) для рекурсивного X имеем: и ;

3) среди рекурсивных m-степеней существует наибольшая, это степень множества X из п.2.

Доказательство. 1. Следует из теоремы.

2. По лемме 4 можно считать, что множество X конечно, а конечно. Тогда существует a . Если и f сводящая функция, то , но по лемме 5 f(a) есть значение некоторой рациональной функции с коэффициентами из , т.е. . Обратно, если существует , то X и [] сводятся друг к другу посредством функции

3. Пусть X конечное рекурсивное множество и . Пусть Y произвольное рекурсивное. Если Y конечно, то по п.1. Если Y коконечно, то по лемме 3, но . Таким образом, упорядочение рекурсивных m-степеней в поле имеет вид:

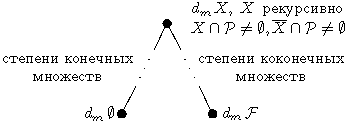
Если в поле достаточно много алгебраических элементов, например, если алгебраически замкнуто, то существует бесконечное число рекурсивных m-степеней.

Следствие 8. Пусть поле алгебраически замкнутое характеристики 0, a рекурсивная m-степень, и не является наибольшей среди рекурсивных. Тогда:

1) существует счетное число рекурсивных степеней, несравнимых с a;

2) существует счетное число попарно несравнимых степеней , таких, что ;

3) существует счетное число попарно несравнимых степеней , таких, что ;

4) порядок на рекурсивных m-степенях плотный.

Доказательство. Пункты 1) - 3) следуют из теоремы 6 и свойств алгебраических расширений полей. Для доказательства 4) рассмотрим рекурсивные множества . Можно считать, что и , причем X и Y не содержат элементов из . Тогда , где , , но .

Список литературы

Ашаев И.В., Беляев В.Я., Мясников А.Г. Подходы к теории обобщенной вычислимости // Алгебра и логика. 32. N 4 (1993). С. 349-386.

Кфури А. Дж., Столбоушкин А.П., Ужичин П. Некоторые открытые вопросы в теории схем программ и динамических логик // УМН. 1989. Т.44. Вып.1 (265). С. 35-55.

Гончаров С.С., Свириденко Д.И. -программирование// Логико-математические проблемы МОЗ (Вычислительные системы. Вып. 107). Новосибирск, 1985. С. 3-29.

Роджерс Х. Теория рекурсивных функций и эффективная вычислимость. М: Мир, 1972.

Blum L., Shub M., Smale S. On a theory of computation and complexity over the real numbers: NP-completeness, recursive functions and universal machines //Bull. Amer. Math. Soc. 1989. V.21. N1. P.1-46.

Friedman H. Algorithmic procedures, generalized Turing algorithms, and elementary recursion theory //Logic Colloquium'69 (R.O. Gandy and C.E.M. Yates, eds). NorthHolland, 1971. Р. 361-390.