Synchronization and Sommerfeld Effect as Typical Resonant Patterns

Kovriguine D.A.

Abstract

This paper presents results of theoretical studies inspired by the problem of reducing the noise and vibrations by using hydraulic absorbers as dampers to dissipate the energy of oscillations in railway electric equipments. The results of experimental trials over these problem and some theoretical calculations, discussed in the text, are demonstrated the ability to customize the damping properties of hydraulic absorbers to save an electric power and protect the equipment itself due to utilizing the synchronous modes of rotation of the rotors.

Key words : Synchronization; resonance, stability, rotor vibrations; dampers.

Introduction

The phenomenon of the phase synchronization, had being first physically described by Huygens, was intensively studied mathematically only since the mid 20-th century, in parallel with significant advances in electronics [1-4]. Fundamental results on the synchronization in terms of the qualitative theory of differential equations and bifurcation theory prove the resonance nature of this phenomenon [5, 6]. Now the application of this theory is widely used to solve pressing practical problems in a wide range of activities, from microelectronics to power supply [7-9]. Now the research interest in advanced fields of the synchronization theory is concentrated, apparently due to the rapid development of new technologies, on studying complex systems with chaotic dynamics, discrete objects and systems with time delay variables. However, in the traditional areas of human activity such as, for instance, energy and transport, there is also noticeable growth of attention in this phenomenon focused on the searching effective ways to save the energy and integrity of power units.

Progressive developments in the scientific researches are constantly improving and expanding in our understanding over the synchronization phenomenon, as a consistent coherent dynamic process. This one occurs usually due to very small, almost imperceptible bonds between the individual elements of the system, which, nevertheless, cause a qualitative change in the dynamical behavior of the object.

The basic equation of the theory of phase synchronization of a pair of oscillators or rotators reads , where is a small frequency (or angular velocity) detuning, is the depth of the phase modulation, is the time. This one being a very simple equation has the general solution in the following form

,

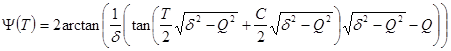where is an arbitrary constant of integration. From this solution follows a simple stability criterion for the stable phase synchronization: . It shows that the phase mismatch must be small, or, accordingly, the parameter of modulation must be sufficiently large, otherwise the synchronization may be destroyed.

A more detailed mathematical study of this problem, referred to a two-rotor system based on an elastic base, turns out that the reduced model is incomplete. Namely, one draws some surprising attention to that the model lacks any description of that element of the system which provides the coupling between the rotors. More detailed studies lead to the following structure of the refined model:

, ,

where describes a measure of the amplitude of oscillations of the elastic foundation. This additional equation appears as a result of the phase modulation of the angular velocity of rotors due to the elastic vibrations of the base. So that, the perturbed rotors, in turn, cause the resonant excitation of vibrations of the base, described by the first equation. In the study of the refined model one can explain that the stable synchronization requires the same condition: . But, one more necessary condition is required, namely, the coefficient of the resonant excitation of vibrations of the base should not exceed the rate of energy dissipation , i. e. . The last restriction significantly alters the stability region of the synchronization in the parameter space of the system that will be demonstrated by some specific computational examples below.

The equations of motion

We consider the motion of two asynchronous drivers mounted on an elastic base. A mathematical model is presented by the following system of widely cited differential equations [10, 11]

;

(1) ;

,

where is the mass of the base, modeled as a rigid body with one degree of freedom, characterized by a linear horizontal displacement , is the coefficient of elasticity of the platform, is the damping coefficient, are the small masses of eccentrics with the eccentricities (radii of inertia), are the moments of inertia of rotors in the absence of imbalance, stands for the driving moments, denotes the resistance moment of the rotor. There is installed the pair of asynchronous drivers (unbalanced rotors) on the platform, whose rotation axes are perpendicular to the direction of base oscillation. The angles of rotation of the rotor are measured from the direction of the axis counter-clockwise. Assume that the moment characteristics of each driver and torque resistance have a simplest form, i. e. , . Here are the constant parameters, respective for the starting points, and stand for the drag coefficients of the rotors. Respectively, the subscript “1” refers to the first driver, while “2” to the second one. If we assume this simple linear model of the moment of static characteristics of the devices, the dimensionless form of eqs. (1) can be rewritten such as follows:

;

(2) ;

,

where appears in the role of the-small parameter of the problem. The parameters and are of order of unity such that and , where and . We introduce new notations: , , (). Here is the oscillation frequency of the base in the absence of the devices, is the dimensionless damping coefficient, is the new dimensionless linear coordinate measured in fractions of the radius of inertia of the eccentrics. The set (2), in contrast to the original equations, depends now on the dimensionless time.

The problem (2) admits an effective study by the method of a small parameter. In order to explore this one, we should transform the system (2) to a standard form of the six equations resolved for the first derivatives. The intermediate steps of this procedure are the follows ones. Firstly, we introduce the new variables, , , , associated with the initial dependent variables by differential relations: , , . Assume that in the set (2). Then one defines the transform to the new dependent variables based on the method of varied constants: , , , , , where , , and are the partial angular velocities of devices. Here , , , , , are the six new variables of the problem. The sense of these new variables: , are the amplitude and phase of base oscillations, respectively, , are the angular accelerations and , are the angular velocities of the rotors. The standard form suitable for further analysis is ready. Because of large records this standard form is not given, but the interested reader can trace in detail the stages of its derivation [12].

Solution of the system in a standard form is solved as transform series in the small parameter :

;

;

(3) ;

;

;

.

Here, the kernel expansion depends upon the slow temporal scales , which characterize the evolution of resonant processes. The variables with superscripts denote small rapidly oscillating correction to the basic evolutionary solution.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--