In addition to the resonance associated with the standard phase synchronization in the system (2) there is one more resonance, when , which apparently has no practical significance, since its angular velocities fall in the zone of instability.

Note that other resonances in the system (2) are absent within the second-order nonlinear approximation theory. The next section investigates these cases are in detail.

Synchronization

After the substitution the expressions (3) into the standard form of equations and the separation between fast and slow motions within the first order approximation theory in the small parameter one obtains the following information on the solution of the system. In the first approximation theory, the slow steady-state motions (when) are the same as in the linearised set, i. e. , ; , ; ; . This means that the slowly varying generalized coordinates , , and , и do not depend within the first approximation analysis upon the physical time nor the slow time . Solutions to the small non-resonant corrections appear as it follows:

(4)

.

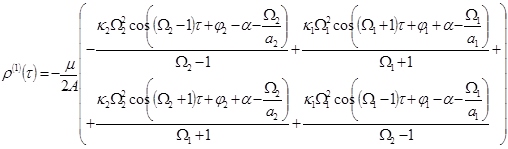
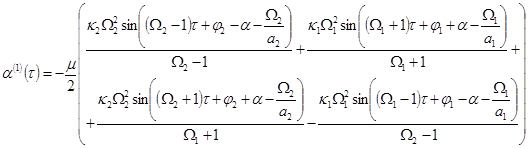
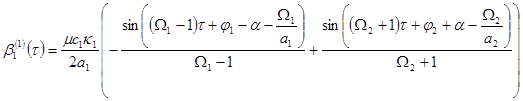
This solution describes a slightly perturbed motion of the base with the same frequencies as the angular velocities of rotors, that is manifested in the appearance of combination frequencies in the expression for the corrections to the amplitude and the phase . Amendments to the angular accelerations , and the velocities, also contain the similar small-amplitude combination harmonics at the difference and sum.

Now the solution of the first-order approximation is ready. This one has not suitable for describing the synchronization effect and call to continue further manipulations with the equations along the small-parameter method. Using the solution (4), after the substitution into eqs. (3), one obtains the desired equation of the second-order nonlinear approximation, describing the synchronization phenomenon of a pair of drivers on the elastic foundation. So that, after the second substitution of the modified representation (3) in the standard form and the separation of motions into slow and fast ones, we obtain the following evolution equations.

(5)

,

where is the new slow variable (), denotes the small detuning of the partial angular velocities, . The coefficients of equations (5) are following:

;

;

;

.

Let the detuning be zero, then these equations are highly simplified up to the full their separation:

(6)

.

Equations (5) represent a generalization of the standard basic equations of the theory of phase synchronization [10], whose structure reads

.(7)

Formally, this equation follows from the generalized model (5) or (6), if we put . The equation (7) has the general solution

,

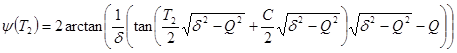where is an arbitrary constant of integration. This solution implies the criterion of the stable phase synchronization:

(8) ,