Статья: Уравнения и характеристики распространения волн реального электромагнитного поля

Здесь важно отметить, что система уравнений (5) иллюстрирует тот непреложный факт, что динамическое существование поля ЭМ векторного потенциала сопровождается неразрывно сопутствующим ему традиционным ЭМ полем. Причем, как установлено, перенос компонентами этих двух полей потока соответствующей физической величины существует, но не посредством обычного волнового процесса, который принципиально невозможен, но он реализуется опосредованно в виде так называемых псевдоволн .

Согласно проведенному здесь анализу, для проводящей среды в асимптотике металлов () распространение волн всех четырех электродинамических составляющих реального ЭМ поля подчиняется теоретически хорошо изученному закону для волн “обычного” ЭМ поля в металлах [2], где все волновые решения имеют вид экспоненциально затухающих в пространстве плоских волн со сдвигом фазы между компонентами на .

Однако вернемся к обсуждению энергетики распространения составляющих реального электромагнитного поля в виде плоских волн в диэлектрической среде без потерь (). Вначале обратимся к закону сохранения электрической энергии , соотношение которого согласно (10) запишется как:

.(12)

Выясним, что представляет собой это выражение для энергии монохроматической электрической волны , полевые компоненты которой, согласно волновым решениям уравнений системы (7), обладая сдвигом фазы на , имеют следующий вид: и . Тогда, подставляя их в соотношение (12), приходим к соотношению:

.

Такой результат вполне удовлетворяет закону сохранения энергии , поскольку усреднение по времени этого соотношения дает

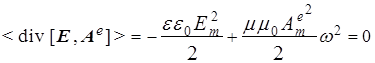, (13)

а потому электрической волной переносится чисто электрическая энергия : , не зависящая от времени и точек пространства.

Соответственно, для магнитного поля , распространяющегося в среде без потерь, уравнение энергетического баланса (11) запишется в виде:

.(14)

Рассмотрим, как выполняется этот закон для плоской монохроматической магнитной волны , полевые компоненты которой, согласно волновым решениям уравнений (8), имеют вид: и . Подставляя их в соотношение (14) и проводя аналогичные рассуждения как при выводе формулы (13), получаем в итоге:

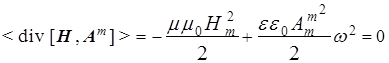. (15)

Итак, в случае магнитного поля снова приходим к физически здравому результату, когда в пространстве без потерь посредством магнитной волны переносится чисто магнитная энергия , не зависящая от времени и точек пространства. Следовательно, распространение магнитной волны также удовлетворяет закону сохранения энергии .

Таким образом, аргументированно показано, что в Природе объективно существует весьма сложное и необычное с точки зрения традиционных представлений вихревое четырехвекторное поле в виде совокупности функционально связанных между собой четырех вихрево-полевых компонент , и , . Это поле, названное реальным электромагнитным полем , реализуется четверкой составляющих его электродинамических полей, состоящих из пар вышеуказанных компонент: электрическое поле с и , магнитное поле с и , электромагнитное поле с и , наконец, поле векторного потенциала с и . При этом описывающие эти поля электродинамические уравнения (5) являются основными уравнениями современной полевой теории электромагнетизма , которые с их следствиями: системами уравнений (1) и (6) - (8) представляют собой фундамент классической электродинамики.

Установлено, что способностью к непосредственному распространению в пространстве в виде волн, отвечающих обычным физическим представлениям о волновом процессе, обладают только волны электрического и магнитного полей за счет наличия у них сдвига фазы колебаний на между их компонентами и , соответственно, и . Реализация же собственно волн ЭМ поля и ЭМ векторного потенциала невозможна в принципе, хотя сами эти поля и их потоки безусловно существуют, но распространяются они опосредованно в виде псевдоволн , поскольку их синфазные компоненты и , соответственно, и являются составной частью компонент электрической и магнитной волн. Именно тем самым все составляющие реального ЭМ поля перемещаются в пространстве совместно посредством единого волнового процесса.

Однако современными методами регистрации электродинамических полей наблюдают только псевдоволны “обычного” ЭМ поля, компоненты и которых синфазно распространяются в пространстве. И хотя конкретное изучение волн остальных обсуждаемых здесь составляющих реального электромагнитного поля только начинается (например, в [8] представлены результаты экспериментального исследования условий возбуждения и распространения в металлах поперечных чисто магнитных волн), объективность их существования и неоспоримая практическая значимость подтверждается, например, принципиальной невозможностью без их посредства реализации такой столь важной физической характеристики ЭМ поля, как способности переноса его энергии.

Как видим, застарелый, возрастом более века парадокс существования волн ЭМ поля и переноса ими энергии этого поля, наконец, успешно и весьма нетривиально разрешен, а результаты проведенных исследований представляют собой серьезное концептуальное развитие основных физических воззрений на структуру и свойства ЭМ поля в классической электродинамике. Кстати, методически серьезных проблем не должно возникнуть, если обсуждаемое здесь реальное электромагнитное поле сохранит за собойи традиционное в электромагнетизменынешнее название – электромагнитное поле с учетом современного развития физических воззрений и его нового содержания. Также с методической точки зрения следует отметить, что настоящий материал вместе с результатами работ [4] может служить концептуальной базой модернизации учебных курсов и создания новых пособий по общей физике, классической электродинамике и родственным им техническим дисциплинам.

Литература

1. Максвелл Дж. К. Трактат об электричестве и магнетизме. Т. I и II. М.: Наука, 1989.

2. Матвеев А.Н. Электродинамика. М.: Высшая школа, 1980.

3. Пирогов А.А. // Электросвязь. 1993. №5. С. 13-14.

4. Сидоренков В.В. // Труды X Всероссийской школы-семинара «Физика и применение микроволн». Секция 2. “Электродинамика”. - М.: МГУ, 2005. С. 2-7; // Необратимые процессы в природе и технике: Сборник научных работ. Выпуск I. - М.: МГТУ им. Н.Э. Баумана, 2005. - С. 127-138; // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2006. № 1. С. 28-37; // Материалы IX Международной конференции «Физика в системе современного образования». Санкт-Петербург: РГПУ, 2007. Секция 1. “Профессиональное физическое образование”. С. 127-129; // Вестник Воронежского государственного технического университета. 2007. Т. 3. № 11. С. 75-82.

5. Докторович З.И. // Заявленное открытие "Магнитные поперечные волны" приоритетная справка 32-ОТ №10247, дата поступления 5 мая 1980 г.

6. Соколов И.В. //УФН. 1991. Т. 161.№ 10. С. 175-190.

7. Чирков А.Г., Агеев А.Н. // ФТТ. 2002. Т. 44. Вып. 1. С. 3-5; 2007. Т. 49. Вып. 7. С. 1217-1221.

8. Сидоренков В.В. // Труды V Всероссийской конференции «Необратимые процессы в природе и технике». Часть I. - М.: МГТУ им. Н.Э. Баумана, 2009. - С. 166-170.