Статья: Задача на собственные значения для вырождающегося уравнения смешанного типа

Таким образом, в области D- найдены частные решения уравнения (1), удовлетворяющие граничному условию (4):

(24)

4. Построение собственных функций задачи Tl. Для нахождения собственных значений и собственных функций задачи Tl , построенную систему функций (17) и (24) удовлетворим условиям склеивания (2) и (5).

Из (17) и (24) вычислим:

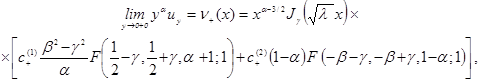
Приравнивая функции

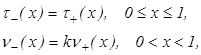
получим систему

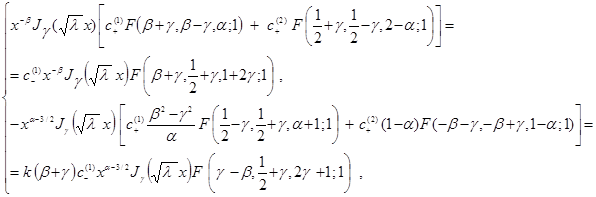
из которой находим коэффициенты и :

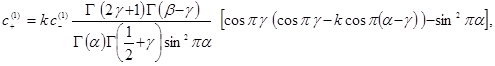(25)

Найденные значения , подставим в равенство (16) и решим его относительно g. Потребуем, чтобы , . Тогда получим:

(27)

Поскольку , то уравнение (27) имеет место, если

Рассмотрим по отдельности случаи и

При уравнение (27) имеет решения или , где . С учетом того, что и , решением (27) будет

При , решением (27) является или , где . С учетом тех же условий получим:

По формулам (25) и (26) находим и при найденных :

где

Из теории бесселевых функций известно [10], что при функция имеет только вещественные нули. Тогда, обозначая через --m-ый корень уравнения (11), находим собственные значения задачи Tl:

Таким образом, построена система собственных функций задачи Tl: