Учебное пособие: Анализ показателей ряда динамики
Чернова А.В., Краснобокая И.А., 2003
Содержание
1. Методические указания по выполнению лабораторной работы
2. Пример выполнения лабораторной работы
3. Задание и порядок выполнения лабораторной работы
Рекомендуемая литература
Приложение
1. Методические указания по выполнению лабораторной работы
Задача изучения изменения анализируемых показателей во времени решается при помощи построения и анализа рядов динамики (временных рядов).
Ряд динамики (динамический ряд) представляет собой ряд числовых значений статистического показателя, расположенных в хронологической последовательности и характеризующих изменение социально-экономических явлений во времени.
В каждом ряду динамики имеются два основных элемента: уровни динамического ряда (обозначаются "Y") и период времени, за который они представлены ("t").
В зависимости от времени, отраженному в динамических рядах, они разделяются на моментные и интервальные.
Моментным рядом динамики называется такой ряд, уровни которого характеризуют состояние явления на определенную дату (момент) времени. Например, ряд, характеризующий динамику численности постоянного населения по состоянию на первое января каждого года.
Интервальным (периодическим) рядом динамики называется такой ряд, уровни которого характеризуют размер явления за конкретный период времени (год, месяц, квартал). Например, ряд, характеризующий динамику выпуска продукции за каждый месяц отчетного года.
Для количественной оценки динамики социально-экономических явлений применяется система показателей ряда динамики, которая может быть представлена следующей группой показателей: абсолютный прирост; темп (коэффициент) роста; темп (коэффициент) прироста; абсолютное значение одного процента прироста.
В основе расчета показателей рядов динамики лежит сопоставление его уровней. В зависимости от применяемого способа сопоставления (базисный или цепной) показатели динамики могут вычисляться на постоянной и переменной базах сравнения.
Для расчета показателей на постоянной базе (базисный способ расчета) каждый уровень ряда сравнивается с одним и тем же базисным уровнем. Исчисляемые при этом показатели называются базисными.
Для расчета показателей на переменной базе (цепной способ расчета) каждый последующий уровень ряда сравнивается с предыдущим. И показатели называются цепными.
Абсолютный прирост характеризует абсолютную скорость роста или снижения сравниваемых уровней, и рассчитывается как разность между последующим и предыдущим уровнем, принятым за базу сравнения. Измеряется в тех же единицах, что и исходная информация.
А = Y1 - Y0 , (1)
где Y1 - значение отчетного уровня ряда динамики;
Y0 - значение базисного уровня ряда динамики.
Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна базисному, т.е. общему приросту за весь промежуток времени.
Темп (коэффициент) роста характеризует относительную скорость роста или снижения уровней ряда динамики и представляет собой отношение каждого последующего уровня к предыдущему, принятому за базу сравнения. Темп роста измеряется в процентах, а коэффициент роста - в долях.
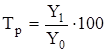 , (2),
, (2), 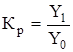 . (3)
. (3)
Между цепными и базисными коэффициентами роста существует взаимосвязь: произведение последовательных цепных коэффициентов роста равно базисному темпу роста последнего периода; частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста.
Темп (коэффициент) прироста показывает, на сколько процентов изменился сравниваемый уровень по отношению к уровню, принятому за базу сравнения:
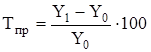 , (4)
, (4)
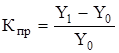 . (5)
. (5)