Учебное пособие: Анализ показателей ряда динамики

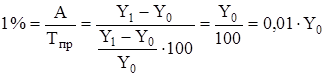. (6)

Для обобщающей характеристики динамики исследуемого явления за ряд периодов определяют различного рода средние показатели. Существуют две категории этих показателей:

1) средние уровни ряда;

2) средние показатели динамики данного ряда.

Метод расчета среднего уровня динамического ряда зависит от вида временного ряда.

В интервальных рядах динамики из абсолютных уровней средний уровень определяется по формуле средней арифметической:

простой (при равных интервалах):

, (7)

где - сумма абсолютных уровней ряда;

n - число уровней.

взвешенной (при неравных интервалах):

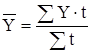, (8)

где Y - уровни ряда динамики, сохраняющиеся без изменения в течение промежутка времени t;

t - длительность интервалов времени (дней, месяцев) между смежными датами.

Для моментного ряда средний уровень определяется с помощью средней хронологической:

простой (для ряда динамики с равностоящими уровнями)

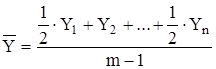, (9)

где Y - уровни периода, за который делается расчет;

m - число уровней.

взвешенной (для ряда динамики с неравностоящими уровнями):

, (10)

где Y_i , Y_n - уровни ряда динамики;

t - интервал времени между уровнями.

При определении средних уровней временного ряда нужно иметь в виду, что средняя будет достаточно надежной характеристикой ряда динамики, если она характеризует период с более или менее стабильными условиями развития. Если же за исследуемый период можно выделить этапы, в течение которых условия развития существенно менялись, то пользоваться общей средней не всегда целесообразно, а предпочтение нужно отдать средним, рассчитанным по отдельным периодам.

Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. При базисном способе расчета, чтобы определить средний абсолютный прирост, для этого определяется разность между конечным У_n и базисным У₀ уровнями изучаемого периода, которая делится на m-1 субпериодов:

, (11)

где m - число уровней ряда динамики в изучаемом периоде, включая базисный. При цепном способе расчета для определения среднего абсолютного прироста сумма цепных абсолютных приростов делится на их число:

, (12)

где n - число цепных абсолютных приростов в изучаемом периоде.