Учебное пособие: Арифметические устройства

3) Сдвиг содержимого регистра-накопителя и регистра-множителя на одну позицию вправо. При этом младший разряд регистра-множителя теряется.

4) Регистр-множитель подает логический 0 на управляющую шину. Этот сигнал блокирует сумматор и сложение не производится.

5) Сдвиг содержимого регистра – накопителя и регистра – множителя на одну позицию вправо.

6) Сложение содержимого регистра – накопителя и регистра – множимого, инициируемое логической 1 младшего разряда регистра – множителя на управляемую шину.

7) Сдвиг содержимого регистра – накопителя и регистра – множителя на одну позицию вправо.

В результате этих шагов произведение (100011) находится сразу в двух регистрах (табл. 15.6).

Таблица 15.6. Пошаговый процесс умножения с использованием операций сложения и сдвига

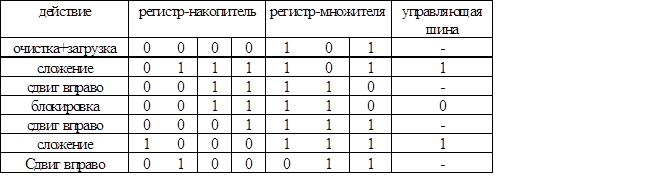
В таблицах 15.5 – 15.6 показаны принципы умножения двумя способами: путем многократного сложения и путем сложений со сдвигами. При этом микропроцессоры могут и не содержать в своих АЛУ умножителей. Конкретный способ умножения можно запрограммировать. Таким образом задавая процессору программу, он выполнит последовательность операций, которая обеспечит умножение двоичных чисел. Благодаря этому существенно уменьшается число электронных схем в центральном процессоре.

15.10. Сложение и вычитание чисел, представленных в дополнительном коде

До сих пор сложение и вычитание производилось над положительными числами. Однако микропроцессоры должны обрабатывать не только положительные, но и отрицательные числа. Используя дополнительный код числа, можно задать как знак числа, так и его абсолютную величину.

Рассмотрим 4 – разрядный дополнительный код. Старший разряд отводится под знак числа: 0 – соответствует положительному числу, 1 – отрицательному. Три разряда отводятся абсолютной величине числа. В табл. 15.7 приведен 4 – разрядный дополнительный код чисел от +7 до –8.

Таблица 15.7. Представление двоичных чисел со знаком.

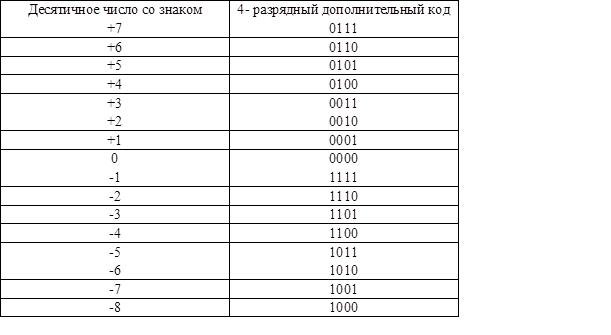
Из табл. 15.7 видно, что дополнительный код положительных чисел совпадает с обычным представлением двоичного числа. Для получения дополнительного кода отрицательного числа нужно сначала сформировать дополнение этого числа до 1, а затем прибавить 1. На рис. 15.23 показана процедура получения дополнительного кода отрицательного числа.

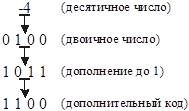
Рис. 15.23. Пример преобразования числа со знаком в дополнительный код

Эта процедура состоит из трех шагов:

1) десятичное число преобразуется к его двоичному эквиваленту соответствующего положительного числа;

2) находится дополнение полученного двоичного числа до 1, путем замены всех единиц на нули и всех нулей на единицы;

3) к полученному дополнению до 1 прибавляется 1. В результате сложения получаем дополнительный код числа.

Процедура перехода от дополнительного кода к двоичному числу, по которому затем определяется десятичное число, показано на рис. 15.24. Обратное преобразование выполняется следующим образом:

1) находим дополнение до 1 для исходного дополнительного кода, путем замены всех единиц на нули и всех нулей на единицы;

к полученному дополнению до 1 прибавляется 1 путем двоичного сложения. В результате получаем искомое двоичное число, но поскольку в старшем разряде дополнительного кода стоит 1, соответствующее десятичное число является отрицательным.

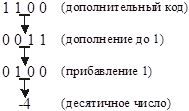
Рис. 15.24. Пример преобразования дополнительного кода в двоичное число

Рассмотрим примеры на сложение и вычитание чисел, представленных в дополнительном коде (рис. 15.25).

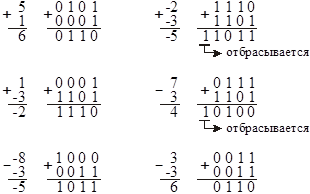
Рис. 15.25. Примеры сложения и вычитания чисел в дополнительном коде