Учебное пособие: Автоматизация технологических процессов и производств

2. Интегральный закон распределения времени до отказа;

3. Дифференциальный закон распределения времени исправной работы устройства до первого отказа;

4. Среднее время безотказной работы (средняя наработка до отказа);

5. Интенсивность отказов.

Прежде чем перейти к показателям надежности, необходимо ввести понятие наработки до отказа.

Наработка до отказа (Т) – случайная величина, представляющая собой длительность работы невосстанавливаемой системы до наступления отказа. Для большей части систем наработка до отказа измеряется единицами времени, но она может измеряться и числом включений, срабатываний, циклов. Очевидно, что для систем, работающих без отключений (кроме отказов), наработка до отказа совпадает с временем безотказной работы.

Основным показателем для количественной оценки безотказности элемента, аппаратуры, приборов и АСУ является вероятность безотказной работы P ( t ) в заданном интервале времени наработки t . Например, Р (1000) =0,99 означает, что из множества элементов данного вида 1% откажет раньше 1000 ч, или что для одного элемента его шансы проработать безотказно 1000 ч составляют 99%. Чем меньше наработка, тем больше P ( t ). Показатель P ( t ) полностью определяет безотказность невосстанавливаемых элементов, но применим также и к восстанавливаемым элементам до первого отказа. Вероятность безотказной работы статистически определяется отношением числа элементов n_i , безотказно проработавших до момента времени t , к числу элементов N работоспособ­ных в начальный момент времени t = 0

P_i *= n_i / N . (2.1)

При значительном увеличении числа элементов N статистиче­ская вероятность P_i * сходится к вероятности

Р ( t )= P { T .> t } (2.2)

где T— наработка до отказа.

Так как исправная работа и отказ — события противоположные, то они связаны очевидным соотношением:

Q ( t )= l - P ( t ) (2.3)

где Q ( t ) —вероятность отказа, или интегральный закон распреде­ления случайной величины — времени работы до отказа.

Статистическое значение вероятности отказа равно отношению числа отказавших элементов к начальному числу испытываемых элементов:

Q_i *=1- n_i / N = ( N - n_i )/ N (2.4)

Производная от вероятности отказа f ( t )= dQ ( t )/ dt = —dP ( t )/ dt есть дифференциальный закон, или плотность распределения слу­чайной величины — времени исправной работы устройства до пер­вого отказа и характеризует скорость снижения вероятности без­отказной работы во времени.

Среднее время безотказной работы Т_ср представляет собой ма­тематическое ожидание времени работы устройства до отказа

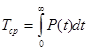(2.5)

Статистическая формула для расчета Т_ср :

(2.6)

где T_i — время безотказной работы I-го устройства; N – общее число элементов.

Интенсивностью отказов l ( t ) называют отношение плотности распределения времени исправной работы к вероятности безотказ­ной работы невосстанавливаемого устройства, которая взята для одного и того же момента времени t. .

l (t)=f(t)/P(t)=-dP/d(t!/P(t). (2.7)

Статистическая формула:

l ( t )*=2( N ₁ - N ₂ )/ t ( N ₁ + N ₂ ) (2.8)

где N ₁ — начальное количество исправных элементов; N₂ — количество исправных устройств через время t .

Интенсивность отказов является наиболее удобной характеристикой безотказности систем и эле­ментов. Как показывает опыт обработки статистических данных по эксплуатации различного оборудования, интенсивность отказов автоматических систем, а также отдельных элементов не может быть аппроксимирована аналитической зависимостью, соответ­ствующей только одному теоретическому закону безотказности.

Обработка большого количества информации об отказах автоматических систем позволила получить общую качественную форму зависимости интенсивности отказов от времени (рис. 2.1).

На кривой, приведенной на рис.2.1 можно выделить три ха­рактерные области:

1) начальных отказов П (область приработки); 2) случайных отказов С (область зрелости ) ; 3) отказов вследствие старения И (область стрости).

В области П интенсивность отказов сначала возрастает, дости­гает максимального значения и затем уменьшается.

Рис. 2.1 Зависимость интенсивности отказов от времени.

Верхняя граница области определяется переходом интенсивности отказов зону постоянных значений. Начальные отказы могут быть обусловлены дефектами материалов, а также главным образом производственными дефектами и некоторыми другими факторами. Причины начальных отказов можно устранить опытной эксплуатацией системы, тренировкой в специальных условиях и режимах работы в течение периода времени, называемого периодом приработки. Продолжительность периода приработки, как показывает опыт, зависит от числа дефектов в системе.

В области случайных отказов интенсивность отказов остается величиной постоянной и определяется сложностью системы, качеством применяемых элементов и режимам их работы, условиями эксплуатации и некоторыми другими факторами. Интервал времени, в течение которого интенсивность отказов постоянна, представляет основной рабочий период систем. В некоторых случаях онсовпадает с минимальным значением производственного ресурса системы. Начало роста интенсивности отказов определяет верхнюю границуобласти случайных отказов и нижнюю границу отказов из-за изношенности. С некоторым допуском возникновение таких отказов может служить критерием долговечности. Следует иметь в виду, что для некоторых систем долговечность может быть меньше, чем сред­нее время безотказной работы системы, рассчитанное как величина, обратная интенсивности отказов. Это обстоятельство следует учи­тывать при назначении гарантийного срока работы системы.

В области И интенсивность отказов сильно возрастает вслед­ствие износа отдельных элементов. В восстанавливаемых системах в области И интенсив­ность отказов имеет колебательный характер, причем амплитуда и частота колебаний зависят от долговечности отдельных элемен­тов и организации профилактических мероприятий при эксплуата­ции системы.

В расчетах надежности необходимо учитывать законы распределения случайной величины – времени работы системы до возникновения отказа. Для дискретных случайных величин применяются биномиальный закон распределения и закон Пуассона . Для непрерывных случайных величин применяются экспоненциальный закон, гамма-распределение, закон Вейбулла, нормальный закон.

Например, закон Пуассона определяет распределение числа m случайного события за время t. Используется для определения вероятности того, что в сложном устройстве за время t произой­дет п отказов.