Для экспоненциального закона Т_ср =0=1/l и удовлетворяются начальные условия Р(0)=1; Q(0)=0, т. е. отчет времени t начинается с момента выяснения исправности изделия.

Графики изменения показателей надежности при экспоненциальном распределении представлены на рис. 2.2.

Рис. 2.2. Показатели надежности при экспоненциальном (А) и нормальном (Б) законе распределения времени безотказной работы.

Основным характерным свойством экспоненциального распределения является то, что вероятность безотказной работы системы на любом интервале времени не зависит от длины этого интервала и не зависит от времени, предшествующей работы системы, т.е. от ее «возраста».

Так как для экспоненциального распределения характерно постоянство интенсивности отказов во времени, то область применения этого закона – системы и элементы, где можно не учитывать ни период приработки, и участок старения и износа (например, многие средства вычислительной техники и регулирования).

Нормальный закон распределения времени исправной работы изделия применяется дли области И l-кривой (рис. 2.1). 3акон применяется, когда отказы системы зависят от большого числа однородных по своему влиянию факторов в процессах износа, старения. Отчет времени t при нормальном законе ведут с начала эксплуатации системы. Интенсивность отказов монотонно возрастает:

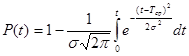; (2.10)

где s - среднеквадратичное отклонение времени безотказной работы системы.

Графики изменения показателей надежности при нормальном распределении представлены на рис. 2.2.

Нормальное распределение, в принципе, описывает поведение случайных величин в диапазоне от (-¥ ; +¥), но так как наработка до отказа является неотрицательной величиной, то используют усеченное нормальное распределение.

Распределение Вейбулла-Гнеденко применяется для описания надежности ряда электронных и механических технических средств, включая период приработки. Это двухпараметрическое распределение, где параметр k определяет вид плотности распределения, m – его масштаб. Так, при k=1 распределение Вейбулла совпадает с экспоненциальным, когда интенсивность отказов постоянна; при k.>1 интенсивность отказов возрастет; при k<1 интенсивность отказов убывает. Функция надежности при распределении Вейбулла имеет вид:

; (2.11)

Рекомендуемая литература для дополнительного чтения:

1. Балакирев В.С., Бадеников В.Я. Надежность технических и программных средств автоматизации. Учеб. пособие для ВУЗов. – Ангарск.: Ангарский технологический институт, 1994, - 64 с.

2. Ястребенецкий М.А., Иванова Г.М. Надежность АСУТП. Учеб. пособие для ВУЗов. – М.: Энергоатомиздат, 1989. – 264 с.

3. Олссон Г. Цифровые системы автоматизации и управления. – М.:

4. Курсовое и дипломное проектирование по автоматизации производственных процессов. Учеб. пособие для ВУЗов. / под ред. И.К. Петрова. – М.: Высшая школа, 1986. – 350 с.

Лекция 3

ПОКАЗАТЕЛИ НАДЕЖНОСТИ ВОССТАНАВЛИВАЕМЫХ СИСТЕМ

После каждого отказа восстанавливаемой системы следует ее восстановлени?