Учебное пособие: Численное решение алгебраических проблем собственных значений
Численное решение алгебраических проблем собственных значений: степенной метод.
Екатеринбург 2006
Введение
Выбор наиболее эффективного метода определения собственных значений и собственных векторов для конкретной инженерной задачи зависит от ряда факторов, таких, как тип уравнений, число искомых собственных значений и их характер. Различают полную (алгебраическую) проблему собственных значений, предполагающую нахождение всех собственных пар {λ, v} матрицы А, и частичную проблему собственных значений, состоящую как правило, в нахождении одного или нескольких собственных чисел λ и, соответствующих им собственных векторов v. Достаточно часто возникают задачи поиска наибольшего и наименьшего по модулю собственных значений квадратной матрицы – знание таких характеристик матрицы позволяют, например, делать заключения о сходимости итерационных процессов, оптимизировать параметры итерационных методов, учитывать влияние на результаты решения алгебраических задач погрешностей исходных данных. Другой пример: имеется матрица размера 5000*5000, в каждой строке которой содержится порядка десяти отличных от нуля элементов (разреженная матрица), и требуется найти только несколько, может быть, четыре или пять, собственных значений. Нахождение всех собственных пар разреженной матрицы представляет собой достаточно сложную вычислительную проблему.
Итерационные методы позволяют находить собственные значения и векторы, минуя процедуру построения характеристического полинома. Отличительной чертой этих методов является то, что собственные значения находятся лишь после определения собственных векторов. Рассмотрим метод, который позволяет найти наибольшее по модулю собственное значение матрицы и соответствующий собственный вектор - степенной метод.
Степенной метод
Классическим методом, который иногда оказывается полезным для больших разреженных систем, хотя и страдает серьезными недостатками, является степенной метод. Предположим, что собственные значения ![]() матрицы
матрицы ![]() вещественны и удовлетворяют условию
вещественны и удовлетворяют условию
![]() (1)
(1)
При заданном векторе ![]() рассмотрим последовательность
рассмотрим последовательность
![]() (2)
(2)
Предположим, что матрица ![]() имеет n линейно независимых собственных векторов
имеет n линейно независимых собственных векторов ![]() соответствующих собственным значениям
соответствующих собственным значениям ![]() (это имеет место, например, в случае симметричной матрицы А). Разложим
(это имеет место, например, в случае симметричной матрицы А). Разложим ![]() по собственным векторам:
по собственным векторам:
![]()
Пусть ![]() , тогда, учитывая (2):
, тогда, учитывая (2):
![]()
Разделим обе части равенства на λ1 k ≠ 0.
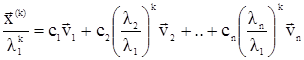
В силу (1) все множители 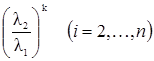 стремятся к нулю при k→ ∞ и вектор
стремятся к нулю при k→ ∞ и вектор ![]() по направлению приближается к собственному вектору
по направлению приближается к собственному вектору ![]() :
:
![]() при k→ ∞, (4)
при k→ ∞, (4)
Если ![]() , то норма вектора
, то норма вектора ![]() будет при этом стремиться к нулю, либо неограниченно возрастать, если
будет при этом стремиться к нулю, либо неограниченно возрастать, если ![]() . На практике вычисляемые векторы нормируют на каждой итерации, а в качестве критерия окончания процесса используют условие:
. На практике вычисляемые векторы нормируют на каждой итерации, а в качестве критерия окончания процесса используют условие:
![]() .
.
Формульно-словесное описание метода:
1. Выбираем ![]() :
: ![]() , k=0, ε – точность вычисления компонент собственного вектора
, k=0, ε – точность вычисления компонент собственного вектора
2. k = k+1
3. Вычисляем ![]()
4. Ищем координату ![]() :
: ![]()
5. Образуем вектор 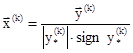
6. Если ![]() , то собственным значением является
, то собственным значением является ![]() ;
;
![]() =
= ![]() ; в противном случае перейти к п. 2.
; в противном случае перейти к п. 2.
Существует модификация степенного метода, которая отличается от предыдущего алгоритма критерием остановки итерационного процесса.
Формульно-словесное описание метода:
1. Выбираем ![]() :
: ![]() , k=0, ε – точность вычисления максимального по модулю собственного значения,
, k=0, ε – точность вычисления максимального по модулю собственного значения, ![]() - некоторый допуск (близость к нулю компонент вектора
- некоторый допуск (близость к нулю компонент вектора ![]() );
);
2. k = k+1;
--> ЧИТАТЬ ПОЛНОСТЬЮ <--