Учебное пособие: Численное решение алгебраических проблем собственных значений

4. Ищем координату : ;

5. Образуем вектор ;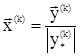

6. Вычисляем для таких i, что , где - допуск;

7. Если , то собственным значением является , где j – число индексов, для которых выполняется условие ; в противном случае перейти к п. 2.

Основным достоинством степенного метода является то, что векторы получаются только с помощью умножения матрицы на вектор (плюс некоторая работа по вычислению нормирующих множителей); никаких преобразований самой матрицы при этом не требуется. Главный недостаток этого метода заключается в том, что он может сходиться очень медленно. Скорость сходимости в первую очередь определяется отношением . Если это отношение по модулю близко к 1, что характерно для многих практических задач, то сходимость будет медленной.

Степенной метод имеет и другие недостатки. Если имеется несколько собственных значений с максимальным модулем, например (а так всегда бывает в случае вещественной матрицы с доминирующей парой комплексно-сопряженных собственных значений), то итерационная последовательность (2) вообще не сходится.

Задание на лабораторную работу

Цель работы: изучение степенных методов расчета максимального по модулю собственного значения и соответствующего собственного вектора квадратной матрицы.

1. Ознакомиться со степенным методом вычисления максимального по модулю собственного значения матрицы A и его модификациями.

2. Составить и отладить программы, рассчитывающие максимальное по модулю собственное значение и соответствующий ему собственный вектор матрицы А произвольной.

3. Элементы матрицы А должны считываться из файла, точность расчета ε вводится с клавиатуры.

4. При проверке работоспособности программ для n=2 и n=3 выполнить ручной расчет собственных значений и собственных векторов матрицы А.

5. Нахождение собственных векторов и собственных значений следует провести, используя самостоятельно составленные и предложенные ниже тестовые примеры:

, ,.

6. При заданной точности расчета ε фиксировать выполненное число итераций k.

7. Составить отчет, который должен содержать следующие разделы:

- описание степенного метода и его модификаций

- описание исходных данных

- схемы-алгоритмов

- тексты программ;

- результаты расчетов тестовых примеров с использованием разработанных программ;

- анализ полученных результатов, выводы по работе;

- список литературы.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Вержбицкий В.М. Основы численных методов: Учебник для вузов. – М.: Высш. шк., 2002. – 840с.

2. Волков Е.А. Численные методы: Учебное пособие. – 3-е изд., испр. – СПб: Лань, 2004. – 248с.

3. Кетков Ю.Л. MATLAB 6: программирование численных методов. – СПб.: БВХ-Петербург, 2004. – 672с.

4. Турчак Л.И. Основы численных методов: Учебное пособие. – М.: Наука. Гл. ред. физ.-мат. лит., 1987. – 320с.