Учебное пособие: Допуски и посадки

Введение

В процессе разработки изделия (машины, агрегата, узла) необходимо исходить из заданного уровня стандартизации и унификации, который определяется коэффициентами применяемости, повторяемости и межпроектной унификации. С повышением значений этих коэффициентов повышается экономическая эффективность разрабатываемого изделия в процессе его производства и эксплуатации. Для повышения уровня стандартизации и унификации необходимо, уже на стадии при проектирования изделия, использовать большее число составных частей, выпускаемых промышленностью, и стремиться к разумному ограничению разработки оригинальных составных частей. При этом, основным вопросом в процессе разработки является точность взаимозаменяемых деталей, узлов и комплектующих изделий, прежде всего по геометрическим параметрам.

Взаимозаменяемость деталей, узлов и агрегатов позволяет осуществить агрегатирование, как один из методов стандартизации, организовать поставку запасных частей, облегчить ремонт, особенно в сложных условиях, сведя его к простой замене изношенных частей.

1.Общие сведения о взаимозаменяемости

Взаимозаменяемость - свойство независимо изготовленных деталей занимать свое место в сборочной единице без дополнительной механической или ручной обработки при сборке, обеспечивая при этом нормальную работу собираемых изделий (узлов, механизмов).

Из самого определения взаимозаменяемости следует, что она является предпосылкой расчленения производства, т.е. независимого изготовления деталей, узлов, агрегатов, которые в последующем собираются последовательно в сборочные единицы, а сборочные единицы - в общую систему (механизм, машину, прибор). Сборку можно вести двумя способами: с подгонкой и без подгонки собираемых деталей или сборочных единиц. Сборку без подгонки применяют в массовом и поточном производствах, а с подгонкой - в единичном и мелкосерийном. При сборке без подгонки детали должны быть изготовлены с необходимой точностью. Однако взаимозаменяемость не обеспечивается одной только точностью геометрических параметров. Необходимо, чтобы материал, долговечность деталей, сборочных единиц и комплектующих изделий был согласован с назначением и условиями работы конечного изделия. Такая взаимозаменяемость называется функциональной , а взаимозаменяемость по геометрическим параметрам является частным видом функциональной взаимозаменяемости.

Взаимозаменяемость бывает полная и неполная, внешняя и внутренняя.

Полная взаимозаменяемость позволяет получить заданные показатели качества без дополнительных операций в процессе сборки.

При неполной взаимозаменяемости во время сборки сборочных единиц и конечных изделий допускаются операции, связанные с подбором и регулировкой некоторых деталей и сборочных единиц. Она позволяет получать заданные технические и эксплуатационные показатели готовой продукции при меньшей точности деталей. При этом, функциональная взаимозаменяемость должна быть только полной, а геометрическая - как полной, так и неполной.

Внешняя взаимозаменяемость - это взаимозаменяемость узлов и комплектующих изделий по эксплуатационным параметрам и присоединительным размерам. Например, замена электродвигателя. Его эксплуатационными параметрами будут - мощность, частота вращения, напряжение, ток; к присоединительным размерам относятся диаметры, число и расположение отверстий в лапах электродвигателя и др.

Внутренняя взаимозаменяемость обеспечивается точностью параметров, которые необходимы для сборки деталей в узлы, а узлов в механизмы. Например, взаимозаменяемость шарикоподшипников или роликов подшипников качения, узлов ведущего и ведомого валов коробки передач и т.д.

Принципы взаимозаменяемости распространяются на детали, сборочные единицы, комплектующие изделия и конечную продукцию.

Взаимозаменяемость обеспечивается точностью параметров изделий, в частности - размерами. Однако, в процессе изготовления неизбежно возникают погрешности Х, численные значения которых находят по формуле

, (0)

где Х - заданное значение размера (параметра);

Х_i - действительное значение этого же параметра.

Погрешности подразделяются на систематические, случайные и грубые (промахи).

Влияние случайных погрешностей на точность измерения можно оценивать методами теории вероятностей и математической статистики. Многочисленными опытами доказано, что распределение случайных погрешностей чаще всего подчиняется закону нормального распределения, который характеризуется кривой Гаусса (рисунок 1).

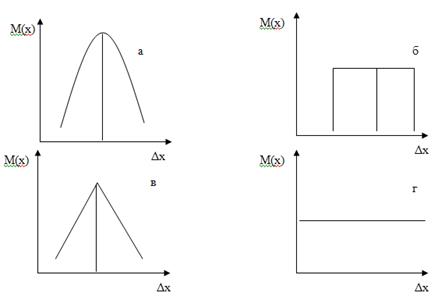
Рисунок 1 - Законы распределения случайных погрешностей

а - нормальный; б – Максвелла; в – треугольника (Симпсона); г - равновероятностный.

Максимальная ордината кривой соответствует среднему значению данного размера (при неограниченном числе измерений называется математическим ожиданием и обозначается М(Х).

По оси абсцисс откладывают случайные погрешности или отклонения от . Отрезки, параллельные оси ординат, выражают вероятность появления случайных погрешностей соответствующей величины. Кривая Гаусса симметрична относительно максимальной ординаты. Поэтому отклонения от одинаковой абсолютной величины, но разных знаков одинаково возможны. Форма кривой показывает, что малые отклонения (по абсолютному значению) появляются значительно чаще, чем большие, а появление весьма больших отклонений практически маловероятно. Поэтому допустимые погрешности ограничиваются некоторыми предельными значениями (V - практическое поле рассеяния случайных погрешностей, равное разности между наибольшими и наименьшими измеренными размерами в партии деталей). Значение определяют из условия достаточной точности при оптимальных затратах на изготовление изделий. При регламентированном поле рассеяния за пределы может выходить не более чем 2,7 % случайных погрешностей. Это значит, что из 100 обработанных деталей может оказаться не более трех бракованных. Дальнейшее уменьшение процента появления бракованных изделий в технико-экономическом отношении не всегда целесообразно, т.к. приводит к чрезмерному увеличению практического поля рассеяния, а, следовательно, увеличению допусков и снижению точности изделий. Форма кривой зависит от методов обработки и измерения изделий; точные методы дают кривую 1, имеющую поле рассеяния V₁ ; методом высокой точности соответствует кривая 2, для которой V₂ <V₁ ; методом низкой точности - кривая 3 (V₃ >V₁ ).

В зависимости от принятого технологического процесса, объема производства и других обстоятельств, случайные погрешности могут распределяться не по закону Гаусса, а по равновероятностному закону (рис.1б), по закону треугольника (рис.1в), по закону Максвелла (рис.1г) и др. Центр группирования случайных погрешностей может совпадать с координатой среднего размера (рис.1а) или смещаться относительно ее (рис.1г).

Нельзя полностью устранить влияние причин, вызывающих погрешности обработки и измерения, можно лишь уменьшить погрешность, применяя более совершенные технологические процессы обработки. Точность размера (любого параметра) называют степень приближения действительного размера к заданному, т.е. точность размера определяется погрешностью. С уменьшением погрешности точность увеличивается и наоборот.

На практике взаимозаменяемость обеспечивается ограничением погрешностей. С уменьшением погрешностей действительные значения параметров, в частности размеров, приближаются к заданным. При небольших погрешностях действительные размеры так мало отличатся от заданных, что их погрешность не ухудшает работоспособность изделий.

2.Допуски и посадки. Понятие о квалитете

Основные термины и определения установлены ГОСТ 25346, ГОСТ 25347, ГОСТ 25348 устанавливают допуски и посадки для размеров менее 1 мм, до 500 мм, свыше 500 до 3150 мм.

Допуск - разность между наибольшими и наименьшими допустимыми значениями какого-либо параметра. Допуски задают на геометрические параметры деталей машин и механизмов (линейные и угловые размеры, на форму и расположение поверхностей и др.), на механические, физико-химические и другие параметры (например, электрическое сопротивление, твердость, содержание химических элементов в материалах). В машиностроении допуски обеспечивают взаимозаменяемость деталей и позволяют осуществлять соединения с различными посадками.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--