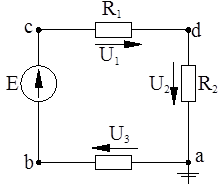Учебное пособие: Электрические измерения
cosj
счетчик ампер-часов
Ah
счетчик ватт-часов
Wh
счетчик вольт-ампер-часов переменный
varh
Лабораторная работа № 2 Исследование неразветвленной и разветвленной электрических цепей постоянного тока
Цель работы: опытная проверка законов Кирхгофа и баланса мощностей в цепях постоянного тока с последовательным и параллельным соединением сопротивлений, построение потенциальной диаграммы.
Теоретические сведения
Электрической цепью называют совокупность устройств, соединенных между собой определенным образом, и образующих путь для электрического тока. В состав цепи могут входить источники электрической энергии, токоприемники, соединительные провода, аппараты управления, защиты и сигнализации, электроизмерительные приборы и т.п. В цепи постоянного тока получение электрической энергии в источниках, ее передача и преобразование в приемниках происходит при неизменных (постоянных) во времени токах и напряжениях.
Любой реальной электрической цепи соответствует эквивалентная схема. Схемой цепи является графическое изображение электрической цепи, содержащее условные обозначения ее элементов и показывающее их соединение. Геометрическая конфигурация схемы характеризуется понятиями ветвь, узел и контур. Ветвь – это участок электрической цепи, вдоль которого протекает один и тот же ток. Узел – это точка соединения трех и более ветвей. Контур – это любой замкнутый путь, образованный ветвями и узлами. Независимым называется контур, который отличается от других контуров схемы одной или несколькими ветвями. Электрическая схема рисунок 2.1 содержит три ветви, два узла и три контура, из которых два любых контура – независимые, а третий – зависимый.
Для анализа и расчета электрических цепей используют законы Ома и Кирхгофа. К узлам схемы применим 1 закон Кирхгофа, согласно которому алгебраическая сумма токов в любом узле электрической цепи равна нулю
![]() (2.1)
(2.1)
При этом токи, текущие к узлу цепи, следует брать с одним знаком, а токи, текущие от узла – с другим знаком, например, для узла-а (см. рис. 2.1) с учетом принятых условно положительных направлений токов в ветвях цепи
I1 – I2 + I3 = 0
К контурам схемы применим 2 закон Кирхгофа, согласно которому алгебраическая сумма э.д.с. в любом замкнутом контуре равна алгебраической сумме падений напряжений на элементах этого контура
![]()
![]() EК =
EК = ![]() IК RК , (2.2)
IК RК , (2.2)
где Rк – сопротивление контура.
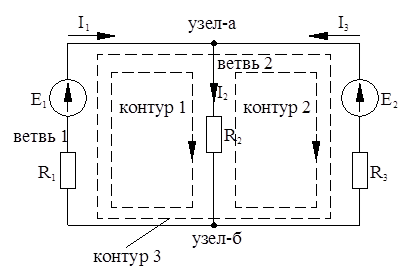
Рисунок 2.1 – Пример схемы электрической цепи
Так для контура 1 (рисунок 2.1)
Е1 = I1 R1 + I2 R2 ,
для контура 3
E1 – E3 = I1 R1 + I3 R3
При обходе контура э.д.с. и токи, направления которых совпадают с принятым направлением обхода, следует считать положительными, а э.д.с. и токи, направленные встречно обходу – отрицательными. Элементы электрической цепи могут быть соединены между собой последовательно, параллельно, в треугольник, в звезду или более сложные схемы. Последовательным соединением сопротивлений называется такая неразветвленная цепь, когда к концу одного сопротивления присоединяется начало второго, к концу второго – начало третьего сопротивления и т.д. В результате, ток протекает последовательно по всем элементам замкнутого контура (рисунок 2.2), не изменяя своей величины.
В цепи с последовательным соединением сопротивлений (рисунок 2.2) по 2 закону Кирхгофа
E = U1 + U2 + U3 ,