Учебное пособие: Физика: механика и термодинамика

Комментарии:

Момент силы: По результатам вычислений М =

По графику 2 М =

Комментарии:

Лабораторная работа №3

ИЗУЧЕНИЕ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ

Цель работы:

Углубить знания по теории гармонических колебаний; освоить методику экспериментальных наблюдений и проверить законы незатухающих гармонических колебаний на примере математического, крутильного или физического маятников; закрепить навыки обработки, оформления и представления экспериментальных результатов.

Часть I. Математический маятник

1.1. Теоретическая часть

Маятник – тело, совершающее колебательное движение под действием упругой или подобной ей, «квазиупругой» силы. Простейший маятник – массивный груз на подвесе, находящийся в поле силы тяжести. Если подвес нерастяжим, размеры груза пренебрежимо малы по сравнению с длиной подвеса и масса нити пренебрежимо мала по сравнению с массой груза, то груз можно рассматривать как материальную точку, находящуюся на неизменном расстоянии l от точки подвеса О . Такой маятник называется математическим .

На груз действуют силы: натяжения нити и тяжести , которые в положении равновесия (точка С, рис.1) компенсируют друг друга . Для возбуждения колебаний маятник выводят из положения равновесия, например, в точку С`. Теперь на него действует сила , направленная к положению равновесия и пропорциональная смещению, маятник обладает избыточной потенциальной энергией mgh по отношению к положению равновесия. Эта энергия обуславливает колебание, происходящее по дуге окружности и описываемое основным уравнением динамики вращательного движения

, (1)

где - результирующий вращающий момент, модуль этого вектора равен ; - угловое ускорение, J = ml² – момент инерции груза относительно оси ОО ^¢ , проходящей через точку подвеса О , перпендикулярно плоскости колебаний (плоскости чертежа).

Дифференциальное уравнение колебаний математического маятника в отсутствии сил сопротивления имеет вид

, (2)

откуда получаем

(3)

Для достаточно малых углов ( j < 5-6 ° ) sin j » j (в радианах), тогда

, (4)

где .

Уравнение (4) представляет собой однородное дифференциальное уравнение второго порядка. Его решением является функция

, (5)

где j ₀ – амплитуда, a ₀ – начальная фаза . В этом можно убедиться, подставив (5) в (4).

Из (5) следует, что угол отклонения маятника из положения равновесия изменяется по гармоническому закону. Величина является циклической частотой собственных колебаний маятника, тогда величина

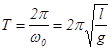(6)

- период колебаний математического маятника.¹

Из выражения (6) следуют три закона колебаний математического маятника:

При малых углах отклонения (sin j » j или j < 6⁰ ) и в отсутствие сторонних сил

1.период колебаний не зависит от массы маятника;

2.период колебаний не зависит от амплитуды;

3.период колебаний определяется формулой .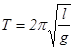

Две из этих закономе