Учебное пособие: Гармонические колебания в параллельном контуре

Т.е. резонансная частота равна частоте собственных колебаний контура. Изменение достигается изменением L или C (чаще).

2) Волновое сопротивление контура

На резонансной частоте, откуда (Ом), т.е. волновое сопротивление контура равно сопротивлению одного из реактивных элементов.

Обычно волновое сопротивление ПК, используемых в электрических цепях, имеет порядок несколько сотен Ом (100500).

3) Добротность контура

По определению , где, следовательно .

Т.к. на резонансной частоте численные значения проводимостей и одинаковые, то добротность можно вычислить по следующей формуле:

, т.о. .

4) Резонансное сопротивление контура, токи в ветвях при резонансе

т.к. при резонансе , то и , т.е. сопротивление контура при резонансе чисто активно и наибольшее по величине.

Действительно, полное сопротивление контура равно:

при , и .

Определим соотношение между током источника и током через реактивный элемент:

, т.е. .

Аналогично можно показать, что.

Вывод :При резонансе токи в ветвях параллельного КК максимальны и в Q раз больше тока источника. Этим и объясняется название режима – резонанс токов .

При резонансной частоте задающий токисточника замыкается через элемент проводимости контура. Токи же в реактивных элементах контура взаимно компенсируют друг друга относительно внешней цепи контура, или, аналогично, что при резонансной частоте круговой ток замыкается через реактивные элементы контура. При этом , а наибольшее по величине. При резонансе напряжение на контуре максимально (). Именно по этому признаку параллельный КК настраивается на резонансную частоту.

4. Комплексные передаточные функции параллельного контура

Выражения для частотных характеристик параллельно колебательного контура относительно напряжения, можно получить из следующей комплексной передаточной функции:

.

Преобразуемзнаменатель:

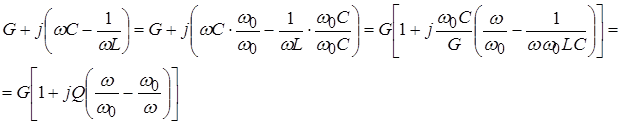т.о. .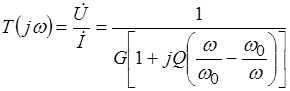

Здесь частотно-зависимым является множитель 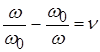называемый относительной расстройкой . Произведение называют обобщенной расстройкой контура .

C учетом этого:.

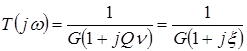Из выражения 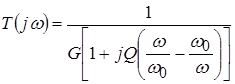получаем

АЧХ : ,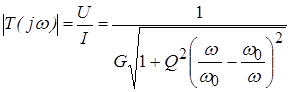

и ФЧХ: .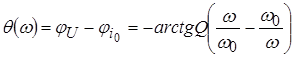

АЧХ называют резонансной характеристикой параллельно колебательного контура. Максимальное значение эта характеристика имеет при резонансной частоте (), .

Резонансную характеристику контура принято нормировать относительно ее максимального значения. Нормированная резонансная характеристика: т.е. отношение амплитуду напряжения при заданной частоте к амплитуде напряжения при резонансе: