Учебное пособие: Гази у зовнішньому силовому полі та основи термодинаміки

2.ККД ідеальної теплової машини має максимальне значення, яке менше від 1, а для реальної ККД – завжди менший ККД циклу Карно.

Поняття про ентропію

Відомо, що внутрішня енергія тіла або системи складається з енергії всіх видів внутрішнього руху в тілі і енергії взаємодії усіх частинок цього тіла або системи. При цьому внутрішня енергія U є однозначною функцією стану тіла або системи. З другого закону термодинаміки випливає, що існує і друга величина, що характеризує однозначно стан термодинамічної системи – це ентропія S.

Щоб пояснити зміст поняття ентропії, розглянемо ізотермічний процес, в якому тіло одержує теплоту Q від нагрівника з температурою Т. Тоді відношення теплоти Q, одержаної в ізотермічному процесі, до температури Т, при якій здійснюється теплопередача, називають приведеною теплотою Q і .

При нагріванні , то при охолодженні . Якщо процес неізотермічний, то його розбивають на такі нескінченно малі ділянки, на яких , і тоді на цій малій ділянці

.

Для довільного процесу із стану А₁ і В /рис. 1б/ одержимо

,

для оборотного колового процесу А а В б А:

.

Можна показати, що для будь-якого оборотного циклу /процес, при якому система з початкового стану переходить в інший і знову повертається в попередній стан без змін не тільки в системі, а і в навколишньому середовищі/. Приведена теплота дорівнює нулю:

.

Це означає, що є повним диференціалом деякої оборотної функції:

Функція, диференціал якої дорівнює приведеній теплоті, називають ентропією системи – це однозначна функція, що характеризує стан системи. Якщо dQ >0 , то і dS >0 – тіло нагрівається і його ентропія зростає, і навпаки.

Розглянемо важливіші властивості ентропії:

1. Ентрорпія системи, що здійснює оборотний цикл, не змінюється:

; .

2. Ентропія замкненої системи при будь-яких процесах в ній не зменшується D S ³ 0 . Знак рівності відноситься до оборотних, а знак нерівносі – до необоротних процесів.

Для приклада обчислимо зміну ентропії ідеального газу. За першим законом термодинаміки і тоді

,

де ,

а .

Враховуючи рівняння , одержимо:

,

і тоді

.

При переході із стану 1 в стан 2 зміна ентропії дорівнює:

.

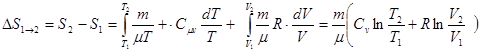Таким чином, зміна ентропії ідеального газу не залежить від виду процесу переходу 1®2, а залежить тільки від початкового /V₁ , Т₁ / і кінцевого стану / V₂ , Т₂ / газу.