Учебное пособие: Графический метод решения химических задач

Зависимость между пропорциональными переменными выражается формулой y=kx линейной функции. Для нашего примера это m(NaSO)=k m(SO) .

Коэффициент пропорциональности – отношение величины молярной массы NaSO к величине молярной массы SO, т.е. k=126:64=1,97.

Для построения графика прямой пропорциональности составляем таблицу значений функции m(NaSO)=k m(SO) .

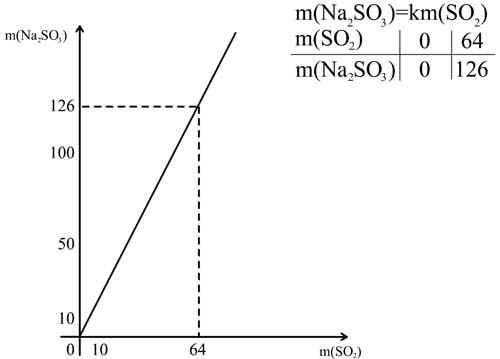
Любая прямая определяется двумя своими точками. В качестве одной из таких точек целесообразно брать начало координат, а вторая точки определяется по соответствующим величинам, найденным по формулу вещества.

m(SO)	0	64
m(NaSO)	0	126

Изобразим зависимость m(NaSO) от m(SO) графически.

Учитель химии

По уравнению реакции:

m(SO)= 1 моль·64 г/моль=64 г

m(NaSO)=1 моль·126 г/моль=126 г

Учитель математики

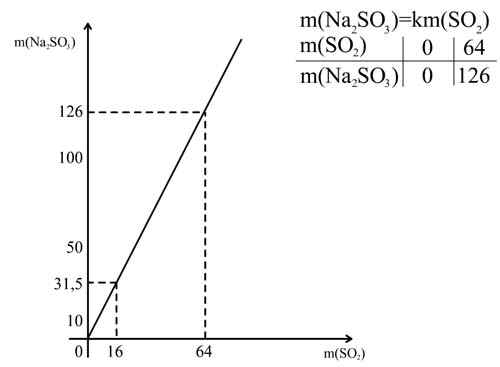
Для решения задачи (см. рис.) на оси абсцисс отмечаем точку, соответствующую числу 16, проводим прямую, параллельную оси ординат, до пересечения с графиком прямой пропорциональности. Из точки пересечения проводим перпендикуляр к оси ординат и получаем точку, которая указывает величину массы сульфита натрия, равную 31,5 г.

Для нахождения более точных значений графики рисуют или в более крупном масштабе, или на миллиметровой бумаге.

Учитель химии

Подобные графические способы химических расчетов широко используются на предприятиях химической промышленности при контроле технологического процесса и анализе готового продукта в химических лабораториях. При химическом анализе сырья и готового продукта используют графики функциональной зависимости для определенной химической реакции.

При решении задач на уроках химии графики практически не применяются из-за неимения дополнительного времени, хотя в 8 классе при изучении темы “Понятие растворимости” можно строить графики растворимости по данным проведенного эксперимента; применять кривые растворимости при нахождении массы растворенного вещества или массы растворителя и при решении других задач.

Графический способ решения задач оказывается более рациональным при решении задач на смеси, смешивание растворов и др.

Задача 2. При растворении в кислоте 2,33 г смеси железа и цинка было получено 896 мл водорода (при н.у.). Вычислите массу каждого из металлов, содержащихся в смеси.

Проанализируем условие задачи. В задаче говорится о взаимодействии смеси металлов с кислотой. Значит, одновременно идут две реакции: цинка с кислотой и железа с кислотой. При этом образуются соответствующие соли, и выделяется водород, суммарный объем которого 0,896 л.

Учитель математики

Решим данное уравнение умножив все его части на произведение 56·65:

65·22,4x + 56·22,4· (2,33-x) = 0,896·56·65

1456x + 2922,752 - 1254,4x = 3261,44

201,6x = 338,688

x = 1,68 г (Fe)

m(Zn) = 2,33 – 1,68 = 0,65 г

Ответ: m(Fe) = 1,68 г