Учебное пособие: Коливальний рух

Уточнимо тепер поняття періоду:

Періодом гармонічного коливального руху називають найменший час, через який всі величини, що характеризують цей рух, набувають початкових значень.

Періоду відповідає зміна фази на :

2. Описання гармонічних коливань. Векторні діаграми.

Крім аналітичного способу описання гармонічних коливань – з допомогою рівняння , існує декілька способів графічного описання гармонічного коливного руху.

а) Плоскі діаграми – це графіки залежності від t (мал 12.1)

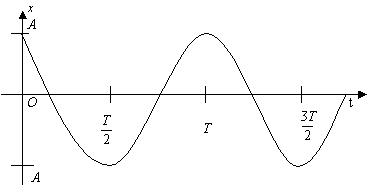
Мал.12.1.

.б) Якщо не цікавляться фазовими співвідношеннями, то зручним є спектральний метод описання гармонічного коливного руху – спектрограма (мал.12.2).

А (або )

v

Мал.12.2

в) Метод векторних діаграм.

На площині вибирають довільний початок О і довільну вісь ОА. Гармонічна величина, що вивчається, наприклад, зміщення, уявляється вектором, який має довжину, пропорційну амплітуді, а кут між ним і віссю ОА дорівнює початковій фазі. В цьому випадку проекція вектора на вісь визначає миттєве зміщення в момент часу, рівне нулю. Якщо тепер уявити, що вектор рівномірно обертається навколо початку О з частотою руху, який вивчається,то в будь-який момент часу його проекція на вісь дає миттєве значення зміщення. (Умовимося вважати додатнім обертанням вектора проти годинникової стрілки).

г) Метод фазових діаграм.

На площині, яку називають фазовою площиною, вибирають прямокутну систему координат. По вісі абсцис відкладають зміщення x, а по вісі ординат – швидкість (у випадку гармонічного коливного руху – “приведену швидкість ” ).

Стан руху в кожний момент часу зображається точкою з координатами , що відповідають даному моменту часу. З плином часу ця точка описує на площині криву , яку називають “фазою траєкторії ”. Для гармонічного коливання руху з (12.1) і (12.4) одержимо:

Це рівняння кола радіусом А з центром початку координат (мал. 12.4). На мал.12.5 – 12.7 наведено для прикладу фазові діаграмми ще для деяких рухів.

Мал 12.4. Мал.12.5.Рывномырний рух.