Учебное пособие: Магнітне поле у вакуумі

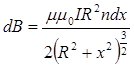. (11.2.20)

Виконаємо заміну змінних у співвідношенні (11.2.20), тобто

, і .

З урахуванням цих позначень одержимо, що

.

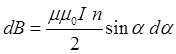Інтегруємо цей вираз у межах зміни кута від ₁ до ₂ . Після інтегрування одержимо

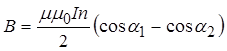. (11.2.21)

Якщо ₁ 0, а ₂ , одержимо соленоїд безмежної довжини. У цьому випадку:

а) індукція магнітного поля на осі довгого соленоїда

. (11.2.22)

б) напруженість магнітного поля на осі довгого соленоїда

. (11.2.23)

3. Магнітний момент контуру із струмом

Для плоского контуру із струмом I магнітний момент визначається співвідношенням:

, (11.3.1)

де I – струм у контурі; S – площа контуру; - нормаль до площини контуру, яка збігається з поступальним рухом правого гвинта, якщо його обертати за напрямком струму у витку.

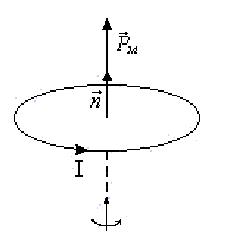
Рис.11.7

Якщо контур із струмом розмістити у зовнішнє магнітне поле, то результуюча сила Ампера, яка діє зі сторони зовнішнього магнітного поля на контур з струмом, буде дорівнювати нулю, тобто

.

У випадку неоднорідного магнітного поля результуючий вектор сили Ампера не буде дорівнювати нулю.

Відповідні розрахунки показують, що в цьому випадку

(11.3.2)

де - похідна вектора в напрямку нормалі або градієнт вектора в напрямку нормалі до контуру; - магнітний момент контуру.