Учебное пособие: Методы исследования операций
4. Особенность операционных исследований состоит в том, что они проводятся комплексно, по многим направлениям. Для проведения такого исследования создается операционная группа. В ее состав входят специалисты разных областей знания: инженеры, математики, экономисты, социологи, психологи. Задачей создания подобных операционных групп является комплексное исследование всего множества факторов, влияющих на решение проблемы, и использование идей и методов различных наук.
Каждое операционное исследование проходит последовательно следующие основные этапы:
1) постановка задачи,
2) построение математической модели,
3) нахождение решения,
4) проверка и корректировка модели,
5) реализация найденного решения на практике.
В самом общем случае математическая модель задачи имеет вид:
найти
max Z=F(x, y) (1.1)
при ограничениях
![]() , (1.2)
, (1.2)
где Z=F(x, y) – целевая функция (показатель качества или эффективность) системы; х — вектор управляемых переменных; у — вектор неуправляемых переменных; Gi(x, y)— функция потребления i-го ресурса; bi — величина i-го ресурса (например, плановый фонд машинного времени группы токарных автоматов в станко-часах).
Определение 1. Любое решение системы ограничений задачи называется допустимым решением.
Определение 2. Допустимое решение, в котором целевая функция достигает своего максимума или минимума называется оптимальным решением задачи.
Для нахождения оптимального решения задачи (1.1)-(1.2) в зависимости от вида и структуры целевой функции и ограничений используют те или иные методы теории оптимальных решений (методы математического программирования).
1. Линейное программирование, если F(x, y), ![]() — линейны относительно переменных х.
— линейны относительно переменных х.
2. Нелинейное программирование, если F(x, y) или ![]() — нелинейны относительно переменных х.
— нелинейны относительно переменных х.
3. Динамическое программирование, если целевая функция F(x, y) имеет специальную структуру, являясь аддитивной или мультипликативной функцией от переменных х.
F(x)=F(x1, x2, …, xn) — аддитивная функция, если F(x1, x2, …, xn)=![]() , и функция F(x1, x2, …, xn) — мультипликативная функция, если F(x1, x2, …, xn)=
, и функция F(x1, x2, …, xn) — мультипликативная функция, если F(x1, x2, …, xn)=![]() .
.
4. Геометрическое программирование, если целевая функция F(x) и ограничения ![]() представляют собой функции вида
представляют собой функции вида
![]()
Математическая модель задачи в этом случае записывается в виде
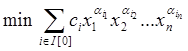
при условиях 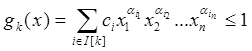 ,
,
![]() ,
,
где I[0]=(m0, m0+1, …, n0); I[k]= (mk, mk+1, …, nk); mk+1=nk+1; m0=1; n0=n.
5. Стохастическое программирование, когда вектор неуправляемых переменных у случаен.
В этом случае математическая модель задачи (1.1—1.2) будет иметь