Учебное пособие: Моделирование экономики

и(Х) < и(У), если и только если Х< Y .

Такая функция называется функцией полезности. Видно, что функция полезности постоянна на каждом классе равноценности, так что ее и вполне правильно представлять себе как функцию, "пересчитывающую" классы равноценности в сторону все большего предпочтения наборов товаров.

Работать с функцией полезности гораздо удобнее, чем с системой.Однако математики выяснили, что если на систему не накладывать никаких ограничений, кроме уже рас­смотренных ранее, а именно, транзитивность, совершенность и рефлексивность, то функции полезности может и не существовать. Тем не менее при некоторых естественных условиях, наложенных на систему функция полезности существует.

Теперь можно сформулировать условия, при которых существует функция полезности.

ТеоремаЕсли система предпочтений непрерыв­на, то существует непрерывная функция полезности.

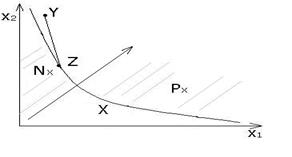Рис.4.1

Надо отметить, что функцияполезности, если она существует, не определяется единственным образом ( рис.4.1).

Основные свойства функции полезности вытекают из ее связи и подчиненности системе предпочтений. Функция полезности неубывающая и дифференцируема.

Состояние рынка, при котором спрос равен предложению называется равновесным, а цена, при которой достигается равенство с проса и предложения -называется р ав новесной ценой

ТеоремaПусть функции спроса и предложения непрерывны и,D(р₀ ) > S(p₀ ) при некоторой цене р₀ ; тогда существует состояние равновесия.

ЛЕКЦИЯ 5

Тема: Типы производственных функций и их свойства

План

1. Типы производственных функций

2. Предельный анализ факторов и однородность производственных функций

3. Эластичность производственных функций

4. Замещение факторов в производственных функциях

5. Производственная функция Кобба-Дугласа

1. Производственные функции можно разделить по количеству используемых переменных, по виду функций и по их свойствам.

Под производственной функцией понимают уравнение, связывающее выпуск продукции и затраты. Производственные функции по количеству переменных различают:

- однофакторные: или ;

- двухфакторные: ;

- многофакторные.

По аналитическому виду:

А) линейные производственные функции

.

Здесь параметры и выражают производительность факторов и , то есть показывают абсолютный прирост производства, когда один фактор остается неизменным, а другой возрастает на единицу. Линейные функции часто используются в краткосрочных и среднесрочных экономических моделях.

б) степенные производственные функции

,