Учебное пособие: Организация пассажирских перевозок

- по условию минимизации пробега свободных мест.

При этом в расчеты могут быть заложены дополнительные условия и ограничения: по загрузке станции, по пропускной способности железнодорожных линий, с учетом пересадок пассажиров или обеспечения заданного уровня беспересадочных сообщений и др.

В курсовом проекте расчет плана формирования производится по наиболее распространенной методике - по условиям освоения пассажиропотока с использованием симплекс-метода.

Для расчета, помимо данных о густоте движения пассажиров, требуется информация о населенности поездов различных назначений, а также сведения об удельных затратах, приходящихся на один поезд каждого назначения. Последние необходимы для экономической оценки вариантов плана формирования поездов.

Населенность поезда рассчитывается по формуле:

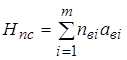, (1.1)

где - число категорий вагонов;

- количество вагонов -й категории в составе пассажирского поезда;

- число мест в вагоне -й категории.

Например, при наличии в составе пассажирского поезда 2 вагонов СВ, 7 купейных, 8 плацкартных и 2 общих вагонов населенность поезда:

тыс.чел.

В курсовом проекте расчет населенности пассажирских поездов следует производить с точностью до «второго знака после запятой».

Рассмотрим пример расчета плана формирования пассажирских поездов для исходных данных, приведенных в табл.1.1.

Для освоения рассчитанной густоты пассажиропотока (табл.1.2) необходимо выполнение следующих ограничений:

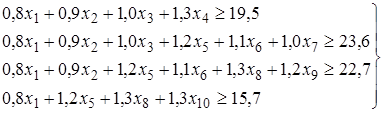. (1.2)

Существует значительное число вариантов плана формирования, при которых обеспечивается освоение расчетных пассажиропотоков. Например, 30 поездов (23,6/0,8) сообщения А-Д обеспечивают освоение расчетного пассажиропотока, однако при этом имеет место пробег свободных мест на участке А-Б в количестве 5 единиц (поездов без пассажиров), а на участке Г-Д - 10 единиц.

Наиболее универсальным критерием для выбора оптимального варианта плана формирования пассажирских поездов является суммарный уровень затрат на перевозки. В этом случае целевая функция будет иметь вид:

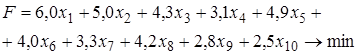. (1.3)

Сформулированная задача может быть решена любым из известных методов линейного программирования. При решении задачи симплекс-методом установлен следующий порядок действий:

1. Выбрать свободные неизвестные, положив их равными нулю и найти соответствующее базисное решение. Если оно окажется недопустимым (отрицательные значения неизвестных), следует найти другой набор свободных неизвестных.

Исходя из сущности задачи ясно, что освоение пассажиропотока возможно при обращении поездов только между соседними станциями, поэтому этот вариант может рассматриваться как базисное решение, которому соответствует следующий набор неизвестных: .

2. Базисные неизвестные и минимизируемую функцию цели необходимо записать в виде разности, в которой уменьшаемое - свободный член. Для условий задачи:

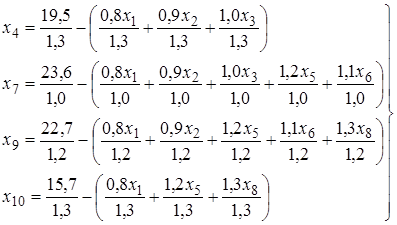. (1.4)

После арифметических преобразований:

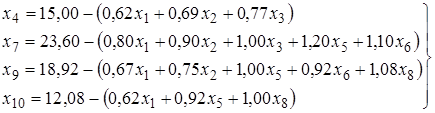. (1.5)

Целевая функция:

.

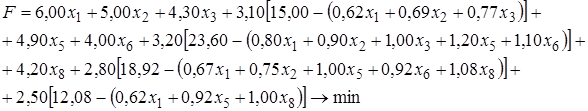После арифметических преобразований:

. (1.6)