Учебное пособие: Растяжение - сжатие
σ3 =
=
=50МПа
Строим эпюры нормальных напряжений.
4. Определяем перемещение свободного конца бруса
∆l =∆l 1 +∆l 2 +∆l 3 
∆l 1 =
=
= – 0,5мм
∆l 2 =
=
= – 0,225мм
∆l 3 =
=
= 0,05мм
∆l = - 0,5 – 0,225 + 0,05 = – 0,675мм
Брус укоротился на 0,675мм
Задача № 2
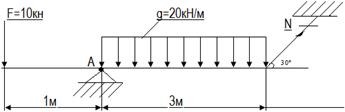
Из условия прочности определить размеры поперечного сечения стержня, удерживающего в равновесии балку, если предел текучести материала σт =320МПа, заданный коэффициент запаса прочности [n] = 2,5. Расчет провести для двух случаев:
1. поперечное сечение стержня – круг;
2. поперечное сечение стержня – квадрат.
Вторая задача может быть решена студентами, если они будут ясно представлять смысл условия прочности при растяжении (сжатии).
Последовательность решения задачи:
Балку, равновесие которой рассматривается, освободить от связей и заменить действия связей их реакциями;
Составить уравнение равновесия, причем принять за точку, относительно которой определяются моменты, точку в которой установлена опора, и определяем продольную силу N;
Определить из условия прочности площадь поперечного сечения стержня;
Определить для двух случаев размеры поперечного сечения стержня.
Для круга – диаметр d;
Для квадрата – сторону a.
Решение
Составляем уравнение равновесия и определяем продольную силу N
Σ m A =0
N∙sin30° ∙3 – 3q∙1,5 + F∙1 = 0
N=
=
= 53,3 кН
2. Определяем допускаемое нормальное напряжение
| [ σ ]= | σ | = = 128 МПа |
| [n] |
3. Определяем площадь поперечного сечения стержня
| σmax | = | N | ≤ [σ]→A ≥ | N | = | 53,3∙103 | =416 мм2 |
| A | [ σ ] | 128 |