Учебное пособие: Систематична похибка опосередкованих вимірювань

Рівняння (4.37) містять у собі шукані величини і числові коефіцієнти . Для визначення m невідомих значень шуканих величин необхідно мати m рівнянь. Тоді результати вимірювань величин і довірчі границі їх похибок можна знайти за методиками обробки результатів опосередкованих вимірювань. Проте, з метою зменшення похибок результатів вимірювань, дослідів проводять дещо більше, ніж число m невідомих величин, тобто .

Оскільки точність вимірювання величин обмежена, то умовні рівняння одночасно не перетворюються в тотожності при жодних значеннях шуканих величин , а отже, не виникає можливості визначення їх істинних значень. Тому задача зводиться до знаходження оцінок шуканих величин , найбільш наближених до істинних значень. Позначимо такі оцінки . Якщо значення підставити в умовні рівняння, то їх ліві частини, в загальному випадку, будуть відрізнятися від правих частин. Такі рівняння і названі умовними. Для одержання тотожності введемо в праві частини умовних рівнянь деякі величини , які називають залишковими похибками умовних рівнянь або відхилами. Звідси маємо

. (4.38)

Для розв’язання системи умовних рівнянь застосовується метод найменших квадратів (МНК), згідно з яким оцінки вибирають так, щоб мінімізувати суму квадратів відхилів

.

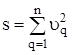Розв’язання задачі в самому загальному випадку, коли умовні рівняння нелінійні, а результати окремих вимірювань корельовані, дещо утруднено. Тому розглянемо окремий випадок, коли умовні рівняння лінійні або приведені до лінійного вигляду, а результати вимірювань величин рівноточні і некорельовані. Тоді оцінки, одержані методом найменших квадратів, будуть обґрунтованими і незміщеними, а при нормальному розподілі результатів вимірювань ще й ефективними. У цьому випадку система рівнянь може бути приведена до вигляду

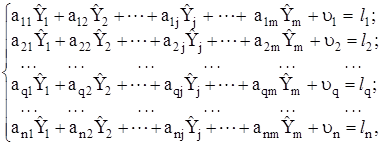(4.39)

де- коефіцієнти, одержані із системи рівнянь після її лінеаризації (якщо вона нелінійна) і підстановки значень величин , причому q - рядок, j - стовпчик;

- постійна величина.

Сума квадратів відхилів визначається із системи рівнянь

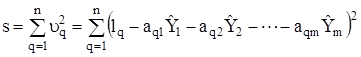
Як відомо, необхідною умовою мінімуму диференціальної функції багатьох змінних, у даному випадку , є виконання рівнянь:

Їх можна розглядати як рівняння відносно величин у математичній статистиці вони називаються нормальними рівняннями.

Використовуючи рівність, знайдемо частинні похідні і прирівняємо їх до нуля:

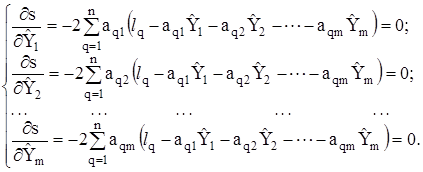
Запишемо одержану систему рівнянь у компактному вигляді

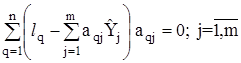
Ця система рівнянь є лінійною відносно шкали величин . Внаслідок розв’язання системи нормальних рівнянь одержують m невідомих величин . Для спрощення запису цієї моделі використовують позначення Гаусса для сум:

; ; .

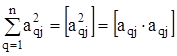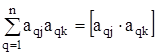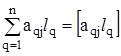З урахуванням цих позначень система нормальних рівнянь набуває вигляду

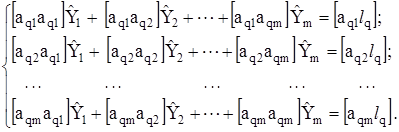
Як відомо, розв’язання такої лінійної системи є лінійними комбінаціями величин :

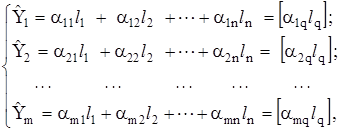
де коефіцієнти знаходять, розв’язуючи систему рівнянь (4.44) за допомогою визначника для кожної з шуканих величин:

,

де ;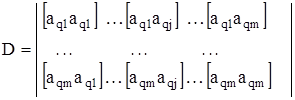

.
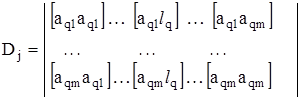