Учебное пособие: Систематична похибка опосередкованих вимірювань

Отже, .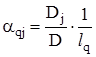

Визначивши з відхили і підставивши їх у рівняння (4.42), одержимо такі рівності:

,

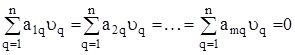що виражають властивості відхилів . Ці рівності застосовуються для перевірки правильності визначення оцінок шуканих величин після розв’язання системи рівнянь.

Визначення оцінок шуканих величин пов’язано з великим обсягом обчислень, який швидко збільшується із збільшенням числа умовних рівнянь. Останнє необхідно для підвищення точності одержаних оцінок. У сучасні дні обробка результатів сумісних і сукупних вимірювань виконується за допомогою ЕОМ за стандартними програмами. Тому точність оцінок істинних значень вимірюваних величин може бути значно підвищена при збільшенні числа умовних рівнянь до кількох десятків і навіть сотень, а в деяких випадках і більше.

Для оцінки точності одержаного розв’язання системи рівнянь звичайно припускають, що точність визначення коефіцієнтів значно вища від точності визначення коефіцієнтів . Це припущення, як правило, виправдане в багатьох практичних випадках. При його виконанні похибки оцінок шуканих величин визначаються тільки дисперсіями результатів вимірювання останніх. А враховуючи, що згідно з рівняннями оцінки є лінійними комбінаціями величин , маємо

,

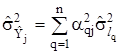де- оцінка дисперсії шуканих величин

- оцінка дисперсії коефіцієнтів .

Якщо припустити, що всі результати спостережень є рівноточними, а отже, всі дисперсії у виразі однакові

,

то оцінка СКВ

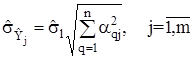
Для обчислення рекомендується досить простий вираз

,

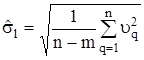в якому залишкові похибки визначають із рівнянь після визначення оцінок згідно з системою рівнянь.

Якщо точність визначення усіх коефіцієнтів системи рівнянь (4.45) приблизно однакова, то оцінку СКВ результату вимірювань величин визначають за формулою

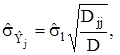
де- алгебраїчні доповнення головного визначника D, які одержують виключенням з нього j-го рядка та j-го стовпця.

З рівнянь випливає, що точність сукупних і сумісних вимірювань залежить від співвідношення числа шуканих величин m і числа умовних рівнянь n. Чим значніша умова , тим точніше результати обробки. Якщо m і n близькі, то результати обробки визначаються з грубими похибками.

Довірчі інтервали для істинних значень усіх вимірюваних величин одержують за розподілом Стьюдента при числі степенів вільності .

Якщо при сукупних і сумісних вимірюваннях умовні рівняння нелінійні, то застосовують їх лінеаризацію.

Таким чином, методика обробки результатів сукупних і сумісних вимірювань така:

1. Записують систему умовних рівнянь при підстановкою експериментальних даних у рівняння початкової залежності.

2. Систему умовних рівнянь приводять до нормального вигляду. Для обчислення коефіцієнтів нормальних рівнянь складають допоміжну табл. 2, яка дозволяє також перевірити правильність визначення шуканих величин.

Таблиця 2.

q			...			...		...		...				...
1			...			...		...		...				...
2			...			...		...		...				...
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
n			...			...		...		...				...
	...			...		...		...		…		...

Визначають оцінки шуканих величин , розв’язуючи систему нормальних рівнянь, для чого використовують один із методів:

а) метод, який ґрунтується на послідовному виключенні невідомих (метод Гаусса);

б) метод із застосуванням визначника.